Question

已知定點A（4，2），點P為拋物線y²=4x上一動點，F為拋物線的焦點，則|PA|+|PF|的最小值為    ．

Answer 1

【答案】分析：設點P在準線上的射影為D，則根據拋物線的定義可知|PF|=|PD|進而把問題轉化為求|PA|+|PD|取得最小，進而可推斷出當D，P，A三點共線時|PA|+|PD|最小，答案可得．
解答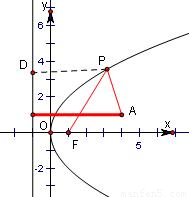：解：設點P在準線上的射影為D，則根據拋物線的定義可知|PF|=|PD|
∴要求|PA|+|PF|取得最小值，即求|PA|+|PD|取得最小
當D，P，A三點共線時|PA|+|PD|最小，為4-（-1）=5．
故故答案為5．
點評：本題考查橢圓的定義、標準方程，以及簡單性質的應用，判斷當D，P，A三點共線時|PA|+|PD|最小，是解題的關鍵．