【題目】
(m-2)x2+(n-8)x+1(m≥0， n≥0）在區間[, 2]上單調遞減，則mn的最大值為（ ）
A.16
B.18
C.25
D.
【答案】B
【解析】m≠2時， 拋物線的對稱軸為x=-
, 據題意，當m>2時，-≥2即2m+n≤12， ∵
≤
≤6, ∴mn≤18, 由2m=n且2m+n=12得m=3, n=6, 當，m<2時， 拋物線開口向下， 根據題意， -≤
即m+2n≤18， ∵
≤≤9, ∴mn≤
, 由2n=m且m+2n=18得m=9>2, 故應舍去使得mn取得最大值，應有m+2n=18(m<2,n>8), 所以mn=(18-2n)n<(18-2x8)x8=16, 所以最大值為18. 選B
【考點精析】本題主要考查了二次函數的性質的相關知識點，需要掌握當
時，拋物線開口向上，函數在
上遞減，在
上遞增；當
時，拋物線開口向下，函數在上遞增，在上遞減才能正確解答此題．
名校名師培優作業本加核心試卷系列答案
全程金卷系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，在正方體
中，點
是棱
上的一個動點，平面
交棱
于點
．給出下列命題：
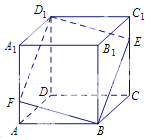
①存在點
，使得
//平面
；
②對于任意的點
，平面
平面
；
③存在點
，使得
平面
；
④對于任意的點
，四棱錐
的體積均不變.
其中正確命題的序號是______．（寫出所有正確命題的序號）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設a,b,c是△ABC的三邊,P: 
, Q:方程x2 +2ax+b2 = 0與方程x2 +2cx－b2 = 0有公共根. 則P是Q的_____.(填：充分不必要條件,必要而不充分條件,充要條件,既不充分也不必要條件)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）=xlnx﹣ax2+（2a﹣1）x，a∈R．
（1）令g（x）=f′（x），求g（x）的單調區間；
（2）已知f（x）在x=1處取得極大值，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體ABCD—A1B1C1D1，
則下列四個命題：
①P在直線BC1上運動時，三棱錐A—D1PC的體積不變；
②P在直線BC1上運動時，直線AP與平面ACD1所成角的大小不變；
③P在直線BC1上運動時，二面角P—AD1—C的大小不變；
④M是平面A1B1C1D1上到點D和C1距離相等的點，則M點的軌跡是過D1點的直線D1A1。
其中真命題的編號是 。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
經過點
、
，并且直線
： 
平分圓
.
（Ⅰ）求圓
的方程；
（Ⅱ）若過點
，且斜率為
的直線
與圓
有兩個不同的交點
.
（ⅰ）求實數
的取值范圍；
（ⅱ）若
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax2﹣ax﹣1（a∈R）．
（1）若對任意實數x，f（x）＜0恒成立，求實數a的取值范圍；
（2）當a＞0時，解關于x的不等式f（x）＜2x﹣3．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，橢圓
的左右頂點分別是
，
為直線
上一點（點在
軸的上方），直線
與橢圓的另一個交點為
，直線
與橢圓的另一個交點為
.
（1）若
的面積是
的面積的
，求直線的方程；
（2）設直線
與直線
的斜率分別為
，求證：
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
