
【題目】某校從參加高三模擬考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六組[90,100),[100,110),…,[140,150]后得到如圖部分頻率分布直方圖.觀察圖形的信息,回答下列問題. 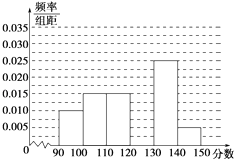
(1)從該校高三模擬考試的成績中隨機抽取一份,利用隨機事件頻率估計概率,求數學分數恰在[120,130)內的頻率;
(2)估計本次考試的中位數;
(3)用分層抽樣的方法在分數段為[110,130)的學生中抽取一個容量為6的樣本,將該樣本看成一個總體,從中任取2人,求至多有1人在分數段[120,130)內的概率.
【答案】
(1)解:分數在[120,130)內的頻率為:
1﹣(0.01+0.015+0.025+0.005)×10=0.3,
∴數學分數恰在[120,130)內的頻率為0.3.
(2)解:由頻率分布直方圖估計本次考試的中位數為:
![]() =
= ![]() .
.
(3)解:由題意[110,120)分數段的人數為60×0.15=9人,
在[120,130)分數段的人數為60×0.3=18人,
∵用分層抽樣的方法在分數段為[110,130)的學生中抽取一個容量為6的樣本,
∴需在[110,120)分數段內抽取兩人,并分別記為m,n,
在[120,130)分數段內抽取4 人,并分別記為a,b,c,d,
設“從樣本中任取2人,至多有1人在分數在[120,130)內”為事件A,
則基本事件共有:n= ![]() 個,
個,
則事件A包含的基本事件個數m=15﹣ ![]() =9個,
=9個,
∴至多有1人在分數段[120,130)內的概率P(A)= ![]() =
= ![]() .
.
【解析】(1)利用頻率分布直方圖能求出分數在[120,130)內的頻率.(2)由頻率分布直方圖能估計本次考試的中位數.(3)[110,120)分數段的人數為9人,在[120,130)分數段的人數為18人,用分層抽樣的方法在分數段為[110,130)的學生中抽取一個容量為6的樣本,需在[110,120)分數段內抽取兩人,在[120,130)分數段內抽取4 人,由此能求出至多有1人在分數段[120,130)內的概率.
【考點精析】利用頻率分布直方圖對題目進行判斷即可得到答案,需要熟知頻率分布表和頻率分布直方圖,是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式,可展示數據的分布情況.通過作圖既可以從數據中提取信息,又可以利用圖形傳遞信息.


科目:高中數學 來源: 題型:
【題目】已知△ABC的三內角A,B,C所對的邊分別是a,b,c,△ABC的面積S= ![]() 且sinA=
且sinA= ![]() .
.
(1)求sinB;
(2)若邊c=5,求△ABC的面積S.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延長A1C1至點P,使C1P=A1C1 , 連接AP交棱CC1于點D.以A1為坐標原點建立空間直角坐標系,如圖所示.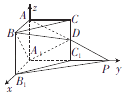
(1)寫出A1、B、B1、C、D、P的坐標;
(2)求異面直線A1B與PB1所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB為圓O的直徑,點E、F在圓O上,AB∥EF,矩形ABCD所在的平面與圓O所在的平面互相垂直.已知AB=2,EF=1.
(Ⅰ)求證:平面DAF⊥平面CBF;
(Ⅱ)求直線AB與平面CBF所成角的大小;
(Ⅲ)當AD的長為何值時,平面DFC與平面FCB所成的銳二面角的大小為60°?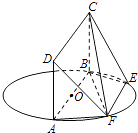
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點A,B是單位圓上的兩點,A,B兩點分別在第一、二象限,點C是圓與x軸正半軸的交點,角∠AOB= ![]() ,若點A的坐標為(
,若點A的坐標為( ![]() ,
, ![]() ),記∠COA=α.
),記∠COA=α. 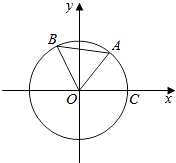
(1)求 ![]() 的值;
的值;
(2)求點B的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分16分)已知數列![]() (
(![]() ,
, ![]() )滿足
)滿足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)當![]() 時,求
時,求![]() 關于
關于![]() 的表達式,并求
的表達式,并求![]() 的取值范圍;
的取值范圍;
(2)設集合![]() .
.
①若![]() ,
, ![]() ,求證:
,求證: ![]() ;
;
②是否存在實數![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都屬于
都屬于![]() ?若存在,請求出實數
?若存在,請求出實數![]() ,
, ![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}中,a1=﹣2,公差d=3;數列{bn}中,Sn為其前n項和,滿足:2nSn+1=2n(n∈N+)
(Ⅰ)記An= ![]() ,求數列An的前n項和S;
,求數列An的前n項和S;
(Ⅱ)求證:數列{bn}是等比數列;
(Ⅲ)設數列{cn}滿足cn=anbn , Tn為數列{cn}的前n項積,若數列{xn}滿足x1=c2﹣c1 , 且xn= ![]() ,求數列{xn}的最大值.
,求數列{xn}的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高一年級學生中隨機抽取50名學生,將他們的期中考試數學成績(滿分100分,成績均為不低于40分的整數)分成六段:[40,50),[50,60),…,[90,100],得到如圖所示的頻率分布直方圖. 
(1)若該校高一年級共有學生1000人,試估計成績不低于60分的人數;
(2)為了幫助學生提高數學成績,學校決定在隨機抽取的50名學生中成立“二幫一”小組,即從成績[90,100]中選兩位同學,共同幫助[40,50)中的某一位同學.已知甲同學的成績為42分,乙同學的成績為95分,求甲、乙恰好被安排在同一小組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 。
。
(1)若f(x)的圖象與g(x)的圖象所在兩條曲線的一個公共點在y軸上,且在該點處兩條曲線的切線互相垂直,求b和c的值。
(2)若a=c=1,b=0,試比較f(x)與g(x)的大小,并說明理由;
(3)若b=c=0,證明:對任意給定的正數a,總存在正數m,使得當x![]() 時,
時,
恒有f(x)>g(x)成立。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com