
���}Ŀ����֪�E�A![]() ��
��![]() �鳣��(sh��)��
�鳣��(sh��)��![]() ���cֱ��
���cֱ��![]() ����ֻ��һ��(g��)�����c(di��n)
����ֻ��һ��(g��)�����c(di��n)![]() ��
��![]() ��
��
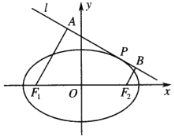
����(d��ng)�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() �r(sh��)����ֱ��
�r(sh��)����ֱ��![]() �ķ��̣�
�ķ��̣�
�����^(gu��)�E�A![]() �ăɽ��c(di��n)
�ăɽ��c(di��n)![]() ��
��![]() ��ֱ��
��ֱ��![]() �Ĵ���������քe��
�Ĵ���������քe��![]() ��
��![]() ������߅��
������߅��![]() ��e�����ֵ����
��e�����ֵ����![]() ��ʾ����
��ʾ����
���𰸡�����![]() ����
����![]() ��
��![]() ��
��
��������
�������ȸ���(j��)�c(di��n)![]() �ڙE�A�����
�ڙE�A�����![]() ��ֵ��Ȼ��(li��n)���E�A�cֱ��
��ֵ��Ȼ��(li��n)���E�A�cֱ��![]() �ķ��̣�����
�ķ��̣�����![]() ���c(di��n)
���c(di��n)![]() ��ֱ��
��ֱ��![]() �����
�����![]() ��
��![]() ��ֵ������⣻
��ֵ������⣻
����(li��n)���E�A�cֱ��![]() �ķ��̣�Ȼ�������Єeʽ���
�ķ��̣�Ȼ�������Єeʽ���![]() ��ȡֵ�������������c(di��n)��ֱ���ľ��x��ʽ���ԭ�c(di��n)��ֱ��
��ȡֵ�������������c(di��n)��ֱ���ľ��x��ʽ���ԭ�c(di��n)��ֱ��![]() �ľ��x
�ľ��x![]() ���������Ǻ���(sh��)���
���������Ǻ���(sh��)���![]() ���Ķ��õ���߅��
���Ķ��õ���߅��![]() ����e�ı��_(d��)ʽ��Ȼ��ͨ�^(gu��)��(g��u)�캯��(sh��)�����ú���(sh��)�Ć��{(di��o)�Լ���������ֵ��
����e�ı��_(d��)ʽ��Ȼ��ͨ�^(gu��)��(g��u)�캯��(sh��)�����ú���(sh��)�Ć��{(di��o)�Լ���������ֵ��
������֪�c(di��n)![]() �ڙE�A
�ڙE�A![]() �ϣ����Եó�
�ϣ����Եó�![]() ��
��
�əE�A![]() �ķ���
�ķ���![]() �cֱ��
�cֱ��![]() (li��n)����
(li��n)����
�ɵ�![]() ��
��
��?y��n)�˷�������ֻ��һ��?/span>![]() ��
��
����![]() ��
��
��![]() �����
�����![]() ��
��![]() ��
��
�Ķ���ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
�����əE�A![]() �cֱ��
�cֱ��![]() (li��n)����
(li��n)����
�ɵ�![]() ��
��
��![]() �ɵ�
�ɵ�![]() ��
��
��![]() ��
��![]() ��֪��
��֪��![]() ��
��
ԭ�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ��
��
![]() ��
��
��?y��n)龀��![]() ��ֱ��
��ֱ��![]() �ϵ�ͶӰ
�ϵ�ͶӰ![]() ��
��
������߅��![]() ����e
����e![]() ��
��
��![]() ����ɵ�
����ɵ�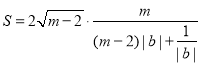 ��
��
��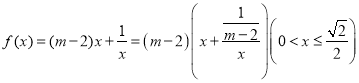 ��
��
�Ɍ�(du��)������(sh��)�Ć��{(di��o)�Կ�֪������(sh��)![]() ��
��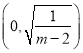 ���f�p����
���f�p����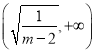 ���f����
���f����
��������(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() ��
��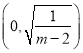 ���f�p����
���f�p����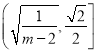 ���f�������Ԯ�(d��ng)
���f�������Ԯ�(d��ng)![]() ����߅��
����߅��![]() ����e
����e![]() ȡ�����ֵ��
ȡ�����ֵ��![]() ��
��
��������(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() ��
��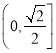 ���f�p�����Ԯ�(d��ng)
���f�p�����Ԯ�(d��ng)![]() ����߅��
����߅��![]() ����e
����e![]() ȡ�����ֵ��
ȡ�����ֵ��![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����������ABC��A1B1C1�У�AB�͂�(c��)��BCC1B1��AC��AB1��
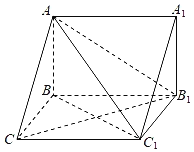
��1�����C��ƽ��ABC1��ƽ��AB1C��
��2����AB��BC��2����BCC1��60����������B��AC1��B1������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����ʽ�M ��ʾ��ƽ��^(q��)��?y��n)?/span>
��ʾ��ƽ��^(q��)��?y��n)?/span>![]() ��������(sh��)
��������(sh��)![]() �ĈD���ϴ��څ^(q��)��
�ĈD���ϴ��څ^(q��)��![]() ��(n��i)���c(di��n)���t��(sh��)��(sh��)
��(n��i)���c(di��n)���t��(sh��)��(sh��)![]() ��ȡֵ�����ǣ� ��
��ȡֵ�����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����߅��ABCD�������Σ�PA��CE��AB=CE![]() PA��PA��ƽ��ABCD.
PA��PA��ƽ��ABCD.
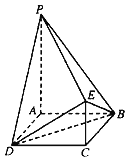
��1���C����PE��ƽ��DBE��
��2��������B��PD��E������ֵ�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D�������![]() �У�
�У�![]() ���侀
���侀![]() ��
��![]() �քe��ƽ��
�քe��ƽ��![]() ��
��![]() ��(n��i)���c(di��n)A��ƽ��
��(n��i)���c(di��n)A��ƽ��![]() ��(n��i)����Ӱǡ�����c(di��n)B���O(sh��)�����
��(n��i)����Ӱǡ�����c(di��n)B���O(sh��)�����![]() ��
��![]() �cƽ��
�cƽ��![]() ���ɽǡ�
���ɽǡ�![]() �cƽ��
�cƽ��![]() ���ɽǵĴ�С�քe��
���ɽǵĴ�С�քe��![]() ���t�� ��
���t�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)�c(di��n)M�����L(zh��ng)��2�������wABCD-A1B1C1D1����AD�����c(di��n)���c(di��n)P����BCC1B1���ڵ�ƽ���(n��i)����ƽ��D1PM�քe�cƽ��ABCD��ƽ��BCC1B1���ɵ��J�������ȣ��t�c(di��n)P���c(di��n)C1����̾��x�ǣ� ��
A.![]() B.
B.![]() C.1D.
C.1D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
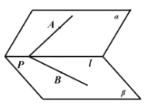
���}Ŀ����D����ƽ����߅��![]() �У�
��![]() ��G��
��G��![]() �����c(di��n)��������
�����c(di��n)��������![]() �cƽ����߅��
�cƽ����߅��![]() ���ڵ�ƽ�滥�ഹֱ��
���ڵ�ƽ�滥�ഹֱ��

��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��2019�����_��(gu��)�H�R���ɱ�ِ����2019��3��31�������ݡ��_���e�У�ij�W(xu��)У���������\(y��n)��(d��ng)���ҿ옷(l��)����呟�������������e�O�M���W(xu��)�����ӱ�ِ�����P(gu��n)���(d��ng)�������˽�W(xu��)���ą��c��r����ȫУ�W(xu��)�����S�C(j��)��ȡ��150���W(xu��)������(du��)�Ƿ��c����r�M(j��n)���ˆ�(w��n)���{(di��o)�飬�y(t��ng)Ӌ(j��)��(sh��)��(j��)���£�
��(hu��)���c | ����(hu��)���c | |
���� | 60 | 40 |
�� | 20 | 30 |
��1������(j��)�ϱ��f(shu��)�����ܷ���97.5%�İ����J(r��n)�酢�c�R����ِ���c�Ԅe���P(gu��n)?
��2���F(xi��n)�ą��c��(w��n)���{(di��o)���҅��cِ�µČW(xu��)���У����ð��Ԅe�ӳ�ӵķ����xȡ8�˅���2019���R���ɱ�ِ־Ը���������(d��ng)��
�����С�Ů�W(xu��)�����xȡ�����ˣ�
������@8�����S�C(j��)�xȡ2�˵�У�V��վ�_չ2019��ِ��������B����ǡ���x��2�������ĸ��ʣ�
����������ʽ��![]() ������
������![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)![]() ���x���ʞ�
���x���ʞ�![]()
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)ֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() ��
��![]() ����߅��ƽ����߅��
����߅��ƽ����߅��![]() ����c(di��n)
����c(di��n)![]() �ڙE�A
�ڙE�A![]() �ϣ����C��ƽ����߅��
�ϣ����C��ƽ����߅��![]() ����e�鶨ֵ.
����e�鶨ֵ.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com