A
分析:由圓的標準方程找出圓心坐標,求出圓心與切點確定的直線方程的斜率,根據兩直線垂直時斜率滿足的關系求出切線方程的斜率,由求出的斜率及切點的坐標寫出切線方程即可.
解答:由圓(x-1)
2+y
2=25,得到圓心坐標為(1,0),
∵過(1,0)和(4,4)兩點的直線方程的斜率為
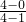
=

,
∴切線方程的斜率為-

,又切點為(4,4),
則切線方程為y-4=-

(x-4),即3x+4y-28=0.
故選A
點評:此題考查了直線與圓的位置關系,涉及的知識有:圓的標準方程,兩直線垂直時斜率滿足的關系,切線的性質,以及直線的點斜式方程,當直線與圓相切時,圓心到直線的距離等于圓的半徑,且圓的切線垂直于過切點的半徑,熟練掌握這些性質是解本題的關鍵.

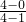 =
= ,
, ,又切點為(4,4),
,又切點為(4,4), (x-4),即3x+4y-28=0.
(x-4),即3x+4y-28=0.
