
(本小題滿分12分)
某港口O要將一件重要物品用小艇送到一艘正在航行的輪船上,在小艇出發時,輪船位于港口的O北偏西30°且與該港口相距20海里的A處,并正以30海里/小時的航行速度沿正東方向勻速行駛. 假設該小艇沿直線方向以v海里/小時的航行速度勻速行駛,經過t小時與輪船相遇.

(Ⅰ)若希望相遇時小艇的航行距離最小,則小艇航行時間應為多少小時?
(Ⅱ)為保證小艇在30分鐘內(含30分鐘)能與輪船相遇,試確定小艇航行速度的最小值;
(I)希望相遇時小艇的航行距離最小,則小艇的航行時間為1/3小時.
(Ⅱ)小艇航行速度的最小值為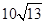 海里/小時。
海里/小時。
【解析】
試題分析:(1)先假設相遇時小艇的航行距離為S,根據余弦定理可得到關系式S= 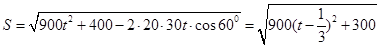
整理后運用二次函數的性質可確定答案.
(2)先假設小艇與輪船在某處相遇,根據余弦定理可得到(vt)2=202+(30t)2-2•20•30t•cos(90°-30°),再由t的范圍可求得v的最小值.
(I)設相遇時小艇的航行距離為S海里,則
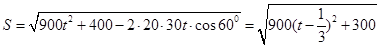 , 故t=1/3時,S min =
, 故t=1/3時,S min =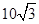 ,
,
答:希望相遇時小艇的航行距離最小,則小艇的航行時間為1/3小時.
(Ⅱ)設小艇與輪船在B處相遇
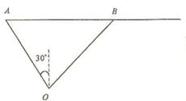
由題意可知,(vt)2 =202 +(30 t)2-2·20·30t·cos(90°-30°),
化簡得: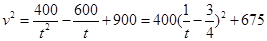
由于0<t≤1/2,即1/t ≥2
所以當 =2時,
=2時,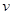 取得最小值
取得最小值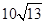 ,
,
即小艇航行速度的最小值為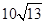 海里/小時。
海里/小時。
考點:本試題主要考查了解三角形、二次函數等基礎知識,考查推理論證能力,抽象概括能力、運算求解能力、應用意識,考查函數與方程思想、數形結合思想、化歸思想
點評:解決該試題的關鍵是能結合余弦定理和函數與不等式的思想求解最值。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中數學 來源: 題型:
(2009湖南卷文)(本小題滿分12分)
為拉動經濟增長,某市決定新建一批重點工程,分別為基礎設施工程、民生工程和產業建設工程三類,這三類工程所含項目的個數分別占總數的![]() 、
、![]() 、
、![]() .現有3名工人獨立地從中任選一個項目參與建設.求:
.現有3名工人獨立地從中任選一個項目參與建設.求:
(I)他們選擇的項目所屬類別互不相同的概率; w.w.w.k.s.5.u.c.o.m ![]()
![]()
(II)至少有1人選擇的項目屬于民生工程的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
某民營企業生產A,B兩種產品,根據市場調查和預測,A產品的利潤與投資成正比,其關系如圖1,B產品的利潤與投資的算術平方根成正比,其關系如圖2,
(注:利潤與投資單位是萬元)
(1)分別將A,B兩種產品的利潤表示為投資的函數,并寫出它們的函數關系式.(2)該企業已籌集到10萬元資金,并全部投入到A,B兩種產品的生產,問:怎樣分配這10萬元投資,才能使企業獲得最大利潤,其最大利潤為多少萬元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com