
【題目】已知函數f(x)=ln(1+x2)+ax.(a≤0)
(1)若f(x)在x=0處取得極值,求a的值;
(2)討論f(x)的單調性;
(3)證明:(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<
)< ![]() (n∈N* , e為自然對數的底數).
(n∈N* , e為自然對數的底數).
【答案】
(1)解:∵ ![]() ,∵x=0使f(x)的一個極值點,則f'(0)=0,
,∵x=0使f(x)的一個極值點,則f'(0)=0,
∴a=0,驗證知a=0符合條件
(2)解:∵ ![]()
①若a=0時,∴f(x)在(0,+∞)單調遞增,在(﹣∞,0)單調遞減;
②若 ![]() 得,當a≤﹣1時,f'(x)≤0對x∈R恒成立,
得,當a≤﹣1時,f'(x)≤0對x∈R恒成立,
∴f(x)在R上單調遞減.
③若﹣1<a<0時,由f'(x)>0得ax2+2x+a>0
∴ ![]()
再令f'(x)<0,可得 ![]()
∴ ![]() 上單調遞增,
上單調遞增,
在 ![]()
綜上所述,若a≤﹣1時,f(x)在(﹣∞,+∞)上單調遞減;
若﹣1<a<0時, ![]() 上單調遞增
上單調遞增 ![]() 上單調遞減;
上單調遞減;
若a=0時,f(x)在(0,+∞)單調遞增,在(﹣∞,0)單調遞減
(3)解:由(2)知,當a=﹣1時,f(x)在(﹣∞,+∞)單調遞減
當x∈(0,+∞)時,由f(x)<f(0)=0
∴ln(1+x2)<x,∴ln[(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )]=ln(1+
)]=ln(1+ ![]() )+ln(1+
)+ln(1+ ![]() )+…+ln(1+
)+…+ln(1+ ![]() )
)
< ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() =
= ![]() (1﹣
(1﹣ ![]() )<
)< ![]() ,∴(1+
,∴(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<
)< ![]() =
= ![]()
【解析】(1)求出f′(x),因為f(x)在x=0時取得極值,所以f'(0)=0,代入求出a即可;(2)分三種情況:a=0;a≤﹣1;﹣1<a<0,令f′(x)>0得到函數的遞增區間;令f′(x)<0得到函數的遞減區間即可;(3)由(2)知當a=﹣1時函數為減函數,所以得到ln(1+x2)<x,利用這個結論根據對數的運算法則化簡不等式的左邊得證即可.
【考點精析】解答此題的關鍵在于理解利用導數研究函數的單調性的相關知識,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減,以及對函數的極值與導數的理解,了解求函數
在這個區間單調遞減,以及對函數的極值與導數的理解,了解求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率e=
的離心率e=![]() ,連接橢圓的四個頂點得到的菱形的面積為4.
,連接橢圓的四個頂點得到的菱形的面積為4.
(1)求橢圓的方程;
(2)設直線![]() 過橢圓的左端點A,與橢圓的另一個交點為B.,AB的垂直平分線交
過橢圓的左端點A,與橢圓的另一個交點為B.,AB的垂直平分線交![]() 軸于點
軸于點![]() ,且
,且![]() ·
·![]() =4,求
=4,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=ax-lnx,a∈R.
(1)當a=1時,求曲線f(x)在點(2,f(2))處的切線方程;
(2)是否存在實數a,使f(x)在區間(0,e]的最小值是3,若存在,求出a的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若f(﹣1)=﹣3,求a
(2)若f(x)的定義域為R,求a的取值范圍;
(3)是否存在實數a,使f(x)在(﹣∞,2)上為增函數?若存在,求出a的范圍?若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C的參數方程為 ![]() ,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線l的極坐標方程為
,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線l的極坐標方程為 ![]() ,A,B兩點的極坐標分別為
,A,B兩點的極坐標分別為 ![]() .
.
(1)求圓C的普通方程和直線l的直角坐標方程;
(2)點P是圓C上任一點,求△PAB面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知無窮數列{an},a1=1,a2=2,對任意n∈N* , 有an+2=an , 數列{bn}滿足bn+1﹣bn=an(n∈N*),若數列 ![]() 中的任意一項都在該數列中重復出現無數次,則滿足要求的b1的值為
中的任意一項都在該數列中重復出現無數次,則滿足要求的b1的值為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)=x2-x+b,且f(log2a)=b,log2f(a)=2(a>0且a≠1).
(1)求a,b的值;
(2)求f(log2x)的最小值及相應x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點P在正方體ABCD﹣A1B1C1D1的表面上運動,且P到直線BC與直線C1D1的距離相等,如果將正方體在平面內展開,那么動點P的軌跡在展開圖中的形狀是( ) 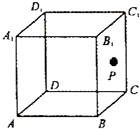
A.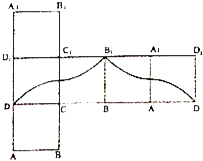
B.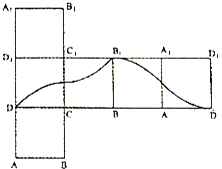
C.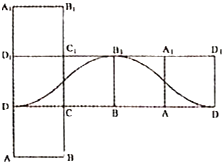
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com