
(1)y=|x|-1,x∈{-2,-1,0,1,2};(2)y=x2+4x+3,(-3≤x≤1);
(3)y=![]() ;(4)y=2x-3+
;(4)y=2x-3+![]() ;(5)y=
;(5)y=![]() .
.
解析:求函數的值域應確定相應的定義域后再根據函數的具體形式及運算確定其值域.(1)本例解析較簡單,故可用“直接法”根據定義域及對應法則得到該函數的值域.(2) 對于二次函數值域的求法,常采用配方法或作出二次函數的圖象求得.(3)對于形如y=![]() (a≠0)型函數值域的求法,常借助反比例函數y=
(a≠0)型函數值域的求法,常借助反比例函數y=![]() (k≠0)的值域解決.(4) 沒有給定自變量的取值范圍,應先考查函數的定義域,再求其值域.對于形如y=ax+b±
(k≠0)的值域解決.(4) 沒有給定自變量的取值范圍,應先考查函數的定義域,再求其值域.對于形如y=ax+b±![]() (a,b,c,d為常數,且ac≠0)的函數值域的求法,常借用整體思想利用“換元法”求值域.(5) 形如y=
(a,b,c,d為常數,且ac≠0)的函數值域的求法,常借用整體思想利用“換元法”求值域.(5) 形如y=![]() 型的函數,由于任一函數的定義域都不可能是空集,所以可將函數化為:(ya2-a1)x2+(yb2-b1)x+yc2-c1=0.當ya2-a1≠0時,上式是關于x的一元二次方程,因此該方程的根的判別式Δ≥0,根據這個不等式可求出函數的值域,當然ya2-a1=0也要考慮.
型的函數,由于任一函數的定義域都不可能是空集,所以可將函數化為:(ya2-a1)x2+(yb2-b1)x+yc2-c1=0.當ya2-a1≠0時,上式是關于x的一元二次方程,因此該方程的根的判別式Δ≥0,根據這個不等式可求出函數的值域,當然ya2-a1=0也要考慮.
解:(1)∵x∈{-2,-1,0,1,2},y=|x|-1,
∴y∈{-1,0,1}.
(2)法一:∵-3≤x≤1,y=x2+4x+3=(x+2)2-1,
∴y∈{y|-1≤y≤8}.
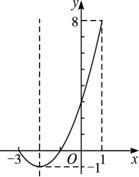
法二:畫出y=x2+4x+3,(-3≤x≤1)的圖象,
如圖所示,當x∈{x|-3≤x≤1}時,得y∈{y|0≤y≤8}.
(3)∵ y=![]() =
=![]() =2+
=2+![]() ,由
,由![]() ≠0,有 y≠2,
≠0,有 y≠2,
∴函數的值域為{y|y∈R,且y≠2}.
(4)∵4x-13≥0,∴x≥![]() .令t=
.令t=![]() ,則得x=
,則得x=![]() .
.
∴y=![]() t2+t+
t2+t+![]() =
=![]() (t+1)2+3,因為x≥
(t+1)2+3,因為x≥![]() ,∴t≥0,因此y≥
,∴t≥0,因此y≥![]() .
.
∴函數 y=2x-3+![]() 的值域為{y|y≥
的值域為{y|y≥![]() }.
}.
(5)由y=![]() 得x∈R,且可化為 (2y-1)x2+2(y+1)x+(y+3)=0,
得x∈R,且可化為 (2y-1)x2+2(y+1)x+(y+3)=0,
∴當 y≠![]() 時,Δ=[2(y+1)]2-4(2y-1)(y+3)≥0.
時,Δ=[2(y+1)]2-4(2y-1)(y+3)≥0.
∴y2+3y-4≤0.∴-4≤y≤1且∴y≠![]() .
.
又當y=![]() 時,代入方程得x=-
時,代入方程得x=-![]() ,滿足條件.
,滿足條件.
∴函數y=![]() 的值域為{y|-4≤y≤1}.
的值域為{y|-4≤y≤1}.


科目:高中數學 來源: 題型:
| 1+sinx |
| 2+cosx |
| ex-e-x |
| ex+e-x |
| 1 |
| x |
| ||
| x+2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com