【題目】在某外國語學校舉行的
(高中生數學建模大賽)中,參與大賽的女生與男生人數之比為
,且成績分布在
,分數在
以上(含)的同學獲獎．按女生、男生用分層抽樣的方法抽取
人的成績作為樣本,得到成績的頻率分布直方圖如圖所示．
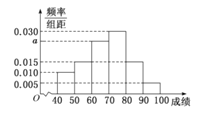
(Ⅰ)求
的值,并計算所抽取樣本的平均值
(同一組中的數據用該組區間的中點值作代表)；
(Ⅱ)填寫下面的
列聯表,并判斷在犯錯誤的概率不超過
的前提下能否認為“獲獎與女生、男生有關”．
女生 | 男生 | 總計 | |
獲獎 |
| ||
不獲獎 | |||
總計 |
| ||
附表及公式：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中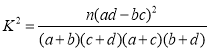
,
．
課時掌控隨堂練習系列答案
一課一練一本通系列答案
浙江之星學業水平測試系列答案科目：高中數學 來源： 題型：
【題目】政府為了穩定房價，決定建造批保障房供給社會，計劃用
萬的價格購得一塊建房用地，在該土地上建
幢樓房供使用，每幢樓的樓層數相同且每層建套每套
平方米，經測算第
層每平方米的建筑造價
(元)與滿足關系式
(其中
為整數且被整除) ，根據某工程師的個人測算可知，該小區只有每幢建
層時每平方米平均綜合費用才達到最低，其中每平方米
.
(1)求的值；
(2)為使該小區平均每平方米的平均綜合費用控制在
元以內，每幢至少建幾層?至多造幾層?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，A（﹣2，0），B（2，0），P為不在x軸上的動點，直線PA，PB的斜率滿足kPAkPB
．
（1）求動點P的軌跡Γ的方程；
（2）若M，N是軌跡Γ上兩點，kMN＝1，求△OMN面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四面體ABCD中，
，
，二面角
的大小為
，
，
．
（1）若
，M是BC的中點，N在線段DC上，
，求證：
平面AMN；
（2）當BP與平面ACD所成角最大時，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xoy中，以坐標原點O為極點，x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為
，過點
的直線l的參數方程為
（為參數），直線l與曲線C交于M、N兩點。
（1）寫出直線l的普通方程和曲線C的直角坐標方程：
（2）若
成等比數列，求a的值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【選修4-4：坐標系與參數方程】
在平面直角坐標系
，已知曲線
（
為參數），在以
原點為極點， 
軸的非負半軸為極軸建立的極坐標系中，直線
的極坐標方程為
。
（1）求曲線
的普通方程和直線
的直角坐標方程；
（2）過點
且與直線
平行的直線
交
于
， 
兩點，求點
到
， 
的距離之積。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
滿足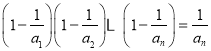
，
.
（1）求數列的通項公式；
（2）已知數列
的通項公式為
，若對于一切，不等式
恒成立，求實數
的取值范圍.
（3）設
，是否存在正整數
，使得數列
中存在某項
滿足
成等差數列？若存在，求出符合題意的的集合；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國南宋數學家楊輝1261年所著的《詳解九章算法》一書里出現了如圖所示的表，即楊輝三角，這是數學史上的一個偉大成就.在“楊輝三角”中，已知第
行的所有數字之和為
，若去除所有為1的項，依次構成數列2，3，3，4，6，4，5，10，10，5，……，則此數列的前56項和為（ ）
A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對某兩名高三學生在連續9次數學測試中的成績（單位：分）進行統計得到折線圖，下面是關于這兩位同學的數學成績分析．
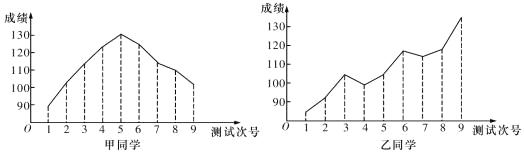
①甲同學的成績折線圖具有較好的對稱性，故平均成績為130分；
②根據甲同學成績折線圖提供的數據進行統計，估計該同學平均成績在區間
內；
③乙同學的數學成績與測試次號具有比較明顯的線性相關性，且為正相關；
④乙同學連續九次測驗成績每一次均有明顯進步．
其中正確的個數為（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
