
| A. | f(x)在(0,$\frac{π}{4}$)上單調遞減 | B. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上單調遞減 | ||
| C. | f(x)在(0,$\frac{π}{4}$)上單調遞增 | D. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上單調遞增 |
分析 利用輔助角化簡函數f(x)=sin(ωx+φ)+cos(ωx+φ)=$\sqrt{2}$sin(ωx+φ$+\frac{π}{4}$)是奇函數,可得φ$+\frac{π}{4}$=kπ,解出φ,直線y=$\sqrt{2}$與函數f(x)的圖象的兩個相鄰交點的距離為$\frac{π}{2}$,可得周期T=$\frac{π}{2}$,求出ω,可得f(x)的解析式,從而判斷各選項即可.
解答 解:化簡函數f(x)=sin(ωx+φ)+cos(ωx+φ)=$\sqrt{2}$sin(ωx+φ$+\frac{π}{4}$)
∵f(x)是奇函數,
∴φ$+\frac{π}{4}$=kπ,k∈Z.即φ=k$π-\frac{π}{4}$.
∵0<φ<π
∴φ=$\frac{3π}{4}$.
又∵直線y=$\sqrt{2}$與函數f(x)的圖象的兩個相鄰交點的距離為$\frac{π}{2}$,
可得周期T=$\frac{π}{2}$,即$\frac{2π}{ω}=\frac{π}{2}$,
∴ω=4.
∴f(x)的解析式為f(x)=$\sqrt{2}$sin(4x+$\frac{3π}{4}$),
令2kπ$-\frac{π}{2}≤$4x+$\frac{3π}{4}$$≤\frac{π}{2}$+2kπ,單調遞增.
可得:$\frac{1}{2}kπ$$-\frac{5π}{16}≤x≤-\frac{π}{16}$+$\frac{1}{2}kπ$,k∈Z.
∴C選項對.D選項不對.
令2kπ+$\frac{π}{2}$≤4x+$\frac{3π}{4}$$≤\frac{3π}{2}$+2kπ,單調遞減.
可得:$\frac{1}{2}kπ$$-\frac{π}{16}≤x≤\frac{3π}{16}$$+\frac{1}{2}kπ$,k∈Z.
∴A,B選項不對.
故選C.
點評 本題主要考查三角函數的圖象和性質,利用三角函數公式將函數進行化簡是解決本題的關鍵.


科目:高中數學 來源: 題型:解答題
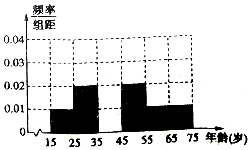 河南多地遭遇年霾,很多學校調整元旦放假時間,提前放假讓學生們在家躲霾.鄭州市根據《鄭州市人民政府辦公廳關于將重污染天氣黃色預警升級為紅色預警的通知》,自12月29日12時將黃色預警升級為紅色預警,12月30日0時啟動Ⅰ級響應,明確要求“幼兒園、中小學等教育機構停課,停課不停學”.學生和家長對停課這一舉措褒貶不一,有為了健康贊成的,有怕耽誤學習不贊成的,某調查機構為了了解公眾對該舉措的態度,隨機調查采訪了50人,將調查情況整理匯總成如表:
河南多地遭遇年霾,很多學校調整元旦放假時間,提前放假讓學生們在家躲霾.鄭州市根據《鄭州市人民政府辦公廳關于將重污染天氣黃色預警升級為紅色預警的通知》,自12月29日12時將黃色預警升級為紅色預警,12月30日0時啟動Ⅰ級響應,明確要求“幼兒園、中小學等教育機構停課,停課不停學”.學生和家長對停課這一舉措褒貶不一,有為了健康贊成的,有怕耽誤學習不贊成的,某調查機構為了了解公眾對該舉措的態度,隨機調查采訪了50人,將調查情況整理匯總成如表:| 年齡(歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
| 贊成人數 | 4 | 6 | 9 | 6 | 3 | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{10}}{5}$ | B. | -$\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | -$\frac{\sqrt{15}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 實驗操作 | |||||
| 不合格 | 合格 | 良好 | 優秀 | ||
| 體能測試 | 不合格 | 0 | 1 | 1 | 1 |
| 合格 | 0 | 2 | 1 | b | |
| 良好 | 1 | a | 2 | 4 | |
| 優秀 | 1 | 1 | 3 | 6 | |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 設橢圓E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的長軸長為6,離心率$e=\frac{{\sqrt{6}}}{3}$,O為坐標原點.
設橢圓E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的長軸長為6,離心率$e=\frac{{\sqrt{6}}}{3}$,O為坐標原點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{4}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com