
【題目】已如橢圓E:![]() (
(![]() )的離心率為
)的離心率為![]() ,點
,點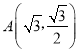 在E上.
在E上.
(1)求E的方程:
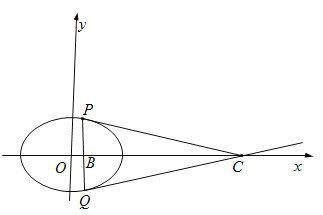
(2)斜率不為0的直線l經過點![]() ,且與E交于P,Q兩點,試問:是否存在定點C,使得
,且與E交于P,Q兩點,試問:是否存在定點C,使得![]() ?若存在,求C的坐標:若不存在,請說明理由
?若存在,求C的坐標:若不存在,請說明理由
【答案】(1)![]() (2)存在x軸上的定點
(2)存在x軸上的定點![]() ,使得
,使得![]()
【解析】
(1)根據橢圓離心率和過的點,得到關于![]() ,
,![]() 的方程組,解得
的方程組,解得![]() ,
,![]() 的值,從而得到橢圓的方程;(2)設存在定點
的值,從而得到橢圓的方程;(2)設存在定點![]() ,對稱性可知設
,對稱性可知設![]() ,根據
,根據![]() ,得到
,得到![]() ,即得
,即得![]() ,直線
,直線![]() 的方程為:
的方程為:![]() 與橢圓聯立,得到
與橢圓聯立,得到![]() ,
,![]() ,從而得到
,從而得到![]() 和
和![]() 的關系式,根據對
的關系式,根據對![]() 恒成立,從而得到
恒成立,從而得到![]() 的值.
的值.
(1)因為橢圓E的離心率![]() ,所以
,所以![]() ①,
①,
點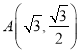 在橢圓上,所以
在橢圓上,所以![]() ②,
②,
由①②解得![]() ,
,![]() .
.
故E的方程為![]() .
.
(2)假設存在定點![]() ,使得
,使得![]() .
.
由對稱性可知,點![]() 必在
必在![]() 軸上,故可設
軸上,故可設![]() .
.
因為![]() ,所以直線
,所以直線![]() 與直線
與直線![]() 的傾斜角互補,因此
的傾斜角互補,因此![]() .
.
設直線![]() 的方程為:
的方程為:![]() ,
,![]() ,
,![]()
由 消去
消去![]() ,得
,得![]() ,
,
![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() .
.
整理得![]() ,
,
所以![]() ,即
,即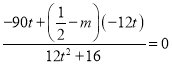 .
.
所以![]() ,即
,即![]() ,對
,對![]() 恒成立,
恒成立,
即![]() 對
對![]() 恒成立,所以
恒成立,所以![]() .
.
所以存在定點![]() ,使得
,使得![]() .
.


科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學名著,它在幾何學中的研究比西方早1000多年,在《九章算術》中,將底面為直角三角形,且側棱垂直于底面的三棱柱稱為塹堵(qian du);陽馬指底面為矩形,一側棱垂直于底面的四棱錐,鱉膈(bie nao)指四個面均為直角三角形的四面體.如圖在塹堵![]() 中,
中,![]() .
.
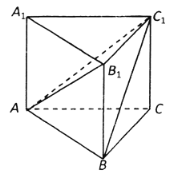
(1)求證:四棱錐![]() 為陽馬;
為陽馬;
(2)若![]() ,當鱉膈
,當鱉膈![]() 體積最大時,求銳二面角
體積最大時,求銳二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() ,與拋物線
,與拋物線![]() 有公共焦點
有公共焦點![]() .
.
(1)求橢圓C1與拋物線![]() 的方程;
的方程;
(2)已知直線![]() 是圓
是圓![]() 的一條切線,與橢圓C1交于
的一條切線,與橢圓C1交于![]() 兩點,若直線
兩點,若直線![]() 斜率存在且不為
斜率存在且不為![]() ,在橢圓C1上存在點
,在橢圓C1上存在點![]() ,使
,使![]() ,其中
,其中![]() 為坐標原點,求實數λ的取值范圍.
為坐標原點,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年電商“雙十一”大戰即將開始.某電商為了盡快占領市場,搶占今年“雙十一”的先機,對成都地區年齡在15到75歲的人群“是否網上購物”的情況進行了調查,隨機抽取了100人,其年齡頻率分布表和使用網上購物的人數如下所示:(年齡單位:歲)
年齡段 |
|
|
|
|
|
|
頻率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
購物人數 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45歲為分界點,根據以上統計數據填寫下面的![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.001的前提下認為“網上購物”與年齡有關?
列聯表,并判斷能否在犯錯誤的概率不超過0.001的前提下認為“網上購物”與年齡有關?
年齡低于45歲 | 年齡不低于45歲 | 總計 | |
使用網上購物 | |||
不使用網上購物 | |||
總計 |
(2)若從年齡在![]() 的樣本中隨機選取2人進行座談,求選中的2人中恰好有1人“使用網上購物”的概率.
的樣本中隨機選取2人進行座談,求選中的2人中恰好有1人“使用網上購物”的概率.
參考數據:
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
參考公式: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com