
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為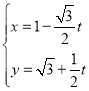 (
(![]() 為參數(shù)),以原點(diǎn)
為參數(shù)),以原點(diǎn)![]() 為極點(diǎn),以x軸正半軸為極軸,建立極坐標(biāo)系,曲線
為極點(diǎn),以x軸正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的極坐標(biāo)方程與曲線
的極坐標(biāo)方程與曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)![]() 、
、![]() 為曲線
為曲線![]() 上位于第一,二象限的兩個(gè)動(dòng)點(diǎn),且
上位于第一,二象限的兩個(gè)動(dòng)點(diǎn),且![]() ,射線
,射線![]() ,
,![]() 交曲線
交曲線![]() 分別于點(diǎn)
分別于點(diǎn)![]() ,
,![]() .求
.求![]() 面積的最小值,并求此時(shí)四邊形
面積的最小值,并求此時(shí)四邊形![]() 的面積.
的面積.
【答案】(1)![]() :
:![]() ,
,![]() :
:![]() .(2)
.(2)![]() 面積的最小值:
面積的最小值:![]() ,四邊形
,四邊形![]() 的面積為:
的面積為:![]() .
.
【解析】
(1)將曲線![]() 消去參數(shù)即可得到
消去參數(shù)即可得到![]() 的普通方程,將
的普通方程,將![]() ,
,![]() 代入曲線
代入曲線![]() 的極坐標(biāo)方程即可;
的極坐標(biāo)方程即可;
(2)由(1)得曲線![]() 的極坐標(biāo)方程,設(shè)
的極坐標(biāo)方程,設(shè)![]() ,
,![]() ,
,![]() ,
,![]() 利用方程可得
利用方程可得![]() ,再利用基本不等式得
,再利用基本不等式得![]() ,根據(jù)題意知
,根據(jù)題意知![]() ,進(jìn)而可得四邊形
,進(jìn)而可得四邊形![]() 的面積.
的面積.
(1)由曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù))
為參數(shù))
消去參數(shù)得![]()
即曲線![]() 的極坐標(biāo)方程為:
的極坐標(biāo)方程為:![]() ,化簡(jiǎn)為:
,化簡(jiǎn)為:![]()
![]()
![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]()
可得![]() ,
,
根據(jù)極坐標(biāo)與直角坐標(biāo)的互化公式:
故:![]() ,
,
曲線![]() 的直角坐標(biāo)方程:
的直角坐標(biāo)方程:![]() .
.
(2)設(shè)![]()
![]()
![]() :
:![]()
![]()
![]() ,
,![]() ,
,
故![]()
根據(jù)均值不等式可得:![]() ,
,
當(dāng)且僅當(dāng)![]() (即
(即![]() )時(shí)取“=”.
)時(shí)取“=”.
![]() ,
,
此時(shí)
故所求四邊形的面積為![]() .
.


 習(xí)題精選系列答案
習(xí)題精選系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 在
在![]() 上的最值;
上的最值;
(2)若對(duì)![]() ,總有
,總有![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線C1:![]() 和圓C2:(x-6)2+(y-1)2=1,過(guò)圓C2上一點(diǎn)P作圓的切線MN交拋物線C,于M,N兩點(diǎn),若點(diǎn)P為MN的中點(diǎn),則切線MN的斜率k>1時(shí)的直線方程為( )
和圓C2:(x-6)2+(y-1)2=1,過(guò)圓C2上一點(diǎn)P作圓的切線MN交拋物線C,于M,N兩點(diǎn),若點(diǎn)P為MN的中點(diǎn),則切線MN的斜率k>1時(shí)的直線方程為( )
A.4x-3y-22=0B.4x-3y-16=0C.2x-y-11+5=0D.4x-3y-26=0
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為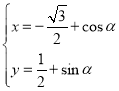 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸,建立極坐標(biāo)系.
為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸,建立極坐標(biāo)系.
(1)設(shè)射線l的極坐標(biāo)方程為![]() ,若射線l與曲線C交于A,B兩點(diǎn),求AB的長(zhǎng);
,若射線l與曲線C交于A,B兩點(diǎn),求AB的長(zhǎng);
(2)設(shè)M,N是曲線C上的兩點(diǎn),若∠MON![]() ,求
,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,將此函數(shù)圖象分別作以下變換,那么變換后的圖象可以與原圖象重合的變換方式有( )
,將此函數(shù)圖象分別作以下變換,那么變換后的圖象可以與原圖象重合的變換方式有( )
①繞著x軸上一點(diǎn)旋轉(zhuǎn)![]() ;②以x軸為軸,作軸對(duì)稱;
;②以x軸為軸,作軸對(duì)稱;
③沿x軸正方向平移;④以x軸的某一條垂線為軸,作軸對(duì)稱;
A.①③B.③④C.②③D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地出現(xiàn)了蟲害,農(nóng)業(yè)科學(xué)家引入了“蟲害指數(shù)”數(shù)列![]() ,
,![]() 表示第
表示第![]() 周的蟲害的嚴(yán)重程度,蟲害指數(shù)越大,嚴(yán)重程度越高,為了治理蟲害,需要環(huán)境整治、殺滅害蟲,然而由于人力資源有限,每周只能采取以下兩個(gè)策略之一:
周的蟲害的嚴(yán)重程度,蟲害指數(shù)越大,嚴(yán)重程度越高,為了治理蟲害,需要環(huán)境整治、殺滅害蟲,然而由于人力資源有限,每周只能采取以下兩個(gè)策略之一:
策略![]() :環(huán)境整治,“蟲害指數(shù)”數(shù)列滿足
:環(huán)境整治,“蟲害指數(shù)”數(shù)列滿足![]() ;
;
策略![]() :殺滅害蟲,“蟲害指數(shù)”數(shù)列滿足
:殺滅害蟲,“蟲害指數(shù)”數(shù)列滿足![]() ;
;
當(dāng)某周“蟲害指數(shù)”小于1時(shí),危機(jī)就在這周解除.
(1)設(shè)第一周的蟲害指數(shù)![]() ,用哪一個(gè)策略將使第二周的蟲害嚴(yán)重程度更小?
,用哪一個(gè)策略將使第二周的蟲害嚴(yán)重程度更小?
(2)設(shè)第一周的蟲害指數(shù)![]() ,如果每周都采用最優(yōu)的策略,蟲害的危機(jī)最快在第幾周解除?
,如果每周都采用最優(yōu)的策略,蟲害的危機(jī)最快在第幾周解除?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓![]() ,動(dòng)點(diǎn)
,動(dòng)點(diǎn)![]() ,線段QF與圓F相交于點(diǎn)P,線段PQ的長(zhǎng)度與點(diǎn)Q到y軸的距離相等.
,線段QF與圓F相交于點(diǎn)P,線段PQ的長(zhǎng)度與點(diǎn)Q到y軸的距離相等.
(Ⅰ)求動(dòng)點(diǎn)Q的軌跡W的方程;
(Ⅱ)過(guò)點(diǎn)![]() 作兩條互相垂直的直線與W的交點(diǎn)分別是M和N(M在N的上方,A,M,N為不同的三點(diǎn)),求向量
作兩條互相垂直的直線與W的交點(diǎn)分別是M和N(M在N的上方,A,M,N為不同的三點(diǎn)),求向量![]() 在y軸正方向上的投影的取值范圍.
在y軸正方向上的投影的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】共享單車又稱為小黃車,近年來(lái)逐漸走進(jìn)了人們的生活,也成為減少空氣污染,緩解城市交通壓力的一種重要手段.為調(diào)查某地區(qū)居民對(duì)共享單車的使用情況,從該地區(qū)居民中按年齡用隨機(jī)抽樣的方式隨機(jī)抽取了![]() 人進(jìn)行問(wèn)卷調(diào)查,得到這
人進(jìn)行問(wèn)卷調(diào)查,得到這![]() 人對(duì)共享單車的評(píng)價(jià)得分統(tǒng)計(jì)填入莖葉圖,如下所示(滿分
人對(duì)共享單車的評(píng)價(jià)得分統(tǒng)計(jì)填入莖葉圖,如下所示(滿分![]() 分):
分):

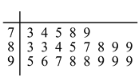
(1)找出居民問(wèn)卷得分的眾數(shù)和中位數(shù);
(2)請(qǐng)計(jì)算這![]() 位居民問(wèn)卷的平均得分;
位居民問(wèn)卷的平均得分;
(3)若在成績(jī)?yōu)?/span>![]() 分的居民中隨機(jī)抽取
分的居民中隨機(jī)抽取![]() 人,求恰有
人,求恰有![]() 人成績(jī)超過(guò)
人成績(jī)超過(guò)![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() (
(![]() )的圖象上的動(dòng)點(diǎn)
)的圖象上的動(dòng)點(diǎn)![]() 到原點(diǎn)
到原點(diǎn)![]() 的距離的平方的最小值為
的距離的平方的最小值為![]() .
.
(1)求![]() 的值;
的值;
(2)設(shè)![]() ,若函數(shù)
,若函數(shù)![]() 有兩個(gè)極值點(diǎn)
有兩個(gè)極值點(diǎn)![]() 、
、![]() ,且
,且![]() ,證明:
,證明:![]() .(參考公式:
.(參考公式:![]() )
)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com