
2013年9月20日是第25個全國愛牙日。某區(qū)衛(wèi)生部門成立了調(diào)查小組,調(diào)查 “常吃零食與患齲齒的關系”,對該區(qū)六年級800名學生進行檢查,按患齲齒和不患齲齒分類,得匯總數(shù)據(jù):不常吃零食且不患齲齒的學生有60名,常吃零食但不患齲齒的學生有100名,不常吃零食但患齲齒的學生有140名.
(1)能否在犯錯概率不超過0.001的前提下,認為該區(qū)學生的常吃零食與患齲齒有關系?
(2)4名區(qū)衛(wèi)生部門的工作人員隨機分成兩組,每組2人,一組負責數(shù)據(jù)收集,另一組負責數(shù)據(jù)處理.求工作人員甲分到負責收集數(shù)據(jù)組,工作人員乙分到負責數(shù)據(jù)處理組的概率.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

(1)學生常吃零食與患齲齒有關系(2)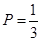
解析試題分析:(1)根據(jù)題意建立相應的列聯(lián)表,根據(jù)公式
科目:高中數(shù)學
來源:
題型:解答題
設袋子中裝有a個紅球,b個黃球,c個藍球,且規(guī)定:取出一個紅球得1分,取出一個黃球得2分,取出一個藍球得3分.
科目:高中數(shù)學
來源:
題型:解答題
某商店試銷某種商品20天,獲得如下數(shù)據(jù):
科目:高中數(shù)學
來源:
題型:解答題
一個口袋中有
科目:高中數(shù)學
來源:
題型:解答題
2014年2月21日,《中共中央關于全面深化改革若干重大問題的決定》明確:堅持計劃生育的基本國策,啟動實施一方是獨生子女的夫婦可生育兩個孩子的政策.為了解某地區(qū)城鎮(zhèn)居民和農(nóng)村居民對“單獨兩孩”的看法,某媒體在該地區(qū)選擇了3600人調(diào)查,就是否贊成“單獨兩孩”的問題,調(diào)查統(tǒng)計的結(jié)果如下表:
科目:高中數(shù)學
來源:
題型:解答題
在高中“自選模塊”考試中,某考場的每位同學都選了一道數(shù)學題,第一小組選《數(shù)學史與不等式選講》的有1人,選《矩陣變換和坐標系與參數(shù)方程》的有5人,第二小組選《數(shù)學史與不等式選講》的有2人,選《矩陣變換和坐標系與參數(shù)方程》的有4人,現(xiàn)從第一、第二兩小組各任選2人分析得分情況.
科目:高中數(shù)學
來源:
題型:解答題
生產(chǎn)A,B兩種元件,其質(zhì)量按測試指標劃分為:指標大于或等于82為正品,小于82為次品,現(xiàn)隨機抽取這兩種元件各100件進行檢測,檢測結(jié)果統(tǒng)計如下:
科目:高中數(shù)學
來源:
題型:解答題
1號箱中有2個白球和4個紅球,2號箱中有5個白球和3個紅球,現(xiàn)隨機地從1號箱中取出一球放入2號箱,然后從2號箱隨機取出一球,問從2號箱取出紅球的概率是多少?
科目:高中數(shù)學
來源:
題型:解答題
第17屆亞運會將于2014年9月18日至10月4日在韓國仁川進行,為了搞好接待工作,組委會招募了16名男志愿者和14名女志愿者,調(diào)查發(fā)現(xiàn),男、女志愿者中分別有10人和6人喜愛運動,其余不喜愛.
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū) 計算
計算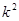 ,查表比較大小即可判斷是否有關
,查表比較大小即可判斷是否有關
(2)古典概型,對四名工作人員編號,利用樹狀圖或者表格的方式列出四選兩個的所有基本事件,求出符合“工作人員甲分到負責收集數(shù)據(jù)組,工作人員乙分到負責數(shù)據(jù)處理組”的基本事件數(shù),根據(jù)古典概型概率的計算公式即可得到相應的概率.
試題解析:(1)由題意可得列聯(lián)表:
因為 不常吃零食 常吃零食 總計 不患齲齒 60 100 160 患齲齒 140 500 640 總計 200 600 800  。
。
所以能在犯錯率不超過0.001的前提下,為該區(qū)學生常吃零食與患齲齒有關系。
(2)設其他工作人員為丙和丁,4人分組的所有情況如下表小組 1 2 3 4 5 6 收集數(shù)據(jù) 甲乙 甲丙 甲丁 乙丙 乙丁 丙丁 處理數(shù)據(jù) 丙丁 

全國名師點撥小學畢業(yè)系統(tǒng)總復習系列答案
中考試題分類精華卷系列答案

名校密卷小升初模擬試卷系列答案
68所名校圖書小學畢業(yè)升學必做的16套試卷系列答案
高分計劃初中文言文提分訓練系列答案
奪冠百分百中考試題調(diào)研系列答案
新閱讀訓練營系列答案
口算題卡每天100道系列答案
中考奪標最新模擬試題系列答案
(1)當a=3,b=2,c=1時,從該袋子中任取(有放回,且每球取到的機會均等)2個球,記隨機變量ξ為取出此兩球所得分數(shù)之和,求ξ分布列;
(2)從該袋子中任取(且每球取到的機會均等)1個球,記隨機變量η為取出此球所得分數(shù).若E(η)= ,V(η)=
,V(η)= ,求a∶b∶c.
,求a∶b∶c.
試銷結(jié)束后(假設該商品的日銷售量的分布規(guī)律不變).設某天開始營業(yè)時由該商品3件,當天營業(yè)結(jié)束后檢查存貨,若發(fā)現(xiàn)存量少于2件,則當天進貨補充至3件,否則不進貨,將頻率視為概率.日銷售量(件) 0 1 2 3 頻數(shù) 1 5 9 5
(1)求當天商店不進貨的概率;
(2)記X為第二天開始營業(yè)時該商品視為件數(shù),求X的分布列和數(shù)學期望. 個白球和
個白球和 個紅球(
個紅球( ,且
,且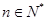 ),每次從袋中摸出兩個球(每次摸球后把這兩個球放回袋中),若摸出的兩個球顏色相同為中獎,否則為不中獎.
),每次從袋中摸出兩個球(每次摸球后把這兩個球放回袋中),若摸出的兩個球顏色相同為中獎,否則為不中獎.
(1)試用含 的代數(shù)式表示一次摸球中獎的概率
的代數(shù)式表示一次摸球中獎的概率 ;
;
(2)若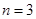 ,求三次摸球恰有一次中獎的概率;
,求三次摸球恰有一次中獎的概率;
(3)記三次摸球恰有一次中獎的概率為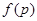 ,當
,當 為何值時,
為何值時,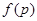 取最大值.
取最大值.
已知在全體樣本中隨機抽取1人,抽到持“反對”態(tài)度的人的概率為0.05.
贊成
反對
無所謂
農(nóng)村居民
2100人
120人
y人
城鎮(zhèn)居民
600人
x人
z人
(1)現(xiàn)在分層抽樣的方法在所有參與調(diào)查的人中抽取360人進行問卷訪談,問應在持“無所謂”態(tài)度的人中抽取多少人?
(2)在持“反對”態(tài)度的人中,用分層抽樣的方法抽取6人,按每組3人分成兩組進行深入交流,求第一組中農(nóng)村居民人數(shù) 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
(1)求選出的4人均為選《矩陣變換和坐標系與參數(shù)方程》的概率;
(2)設X為選出的4個人中選《數(shù)學史與不等式選講》的人數(shù),求X的分布列和數(shù)學期望.
(1)試分別估計元件A、元件B為正品的概率;測試指標 [70,76) [76,82) [82,88) [88,94) [94,100] 元件A 8 12 40 32 8 元件B 7 18 40 29 6
(2)生產(chǎn)一件元件A,若是正品可盈利50元,若是次品則虧損10元;生產(chǎn)一件元件B,若是正品可盈利100元,若是次品則虧損20元,在(1)的前提下:
(i)求生產(chǎn)5件元件B所獲得的利潤不少于300元的概率;
(ii)記X為生產(chǎn)1件元件A和1件元件B所得的總利潤,求隨機變量X的分布列和數(shù)學期望.
(1)根據(jù)調(diào)查數(shù)據(jù)制作2×2列聯(lián)表;
(2)根據(jù)列聯(lián)表的獨立性檢驗,能否認為性別與喜愛運動有關?
(參考公式:參考數(shù)據(jù) 當 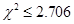 時,無充分證據(jù)判定變量
時,無充分證據(jù)判定變量 有關聯(lián),可以認為兩變量無關聯(lián);
有關聯(lián),可以認為兩變量無關聯(lián);當  時,有
時,有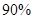 把握判定變量
把握判定變量 有關聯(lián);
有關聯(lián);當 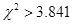 時,有
時,有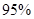 把握判定變量
把握判定變量 有關聯(lián);
有關聯(lián);當 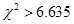 時,有
時,有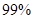 把握判定變量
把握判定變量 有關聯(lián).
有關聯(lián). ,其中
,其中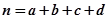 .)
.)
版權(quán)聲明:本站所有文章,圖片來源于網(wǎng)絡,著作權(quán)及版權(quán)歸原作者所有,轉(zhuǎn)載無意侵犯版權(quán),如有侵權(quán),請作者速來函告知,我們將盡快處理,聯(lián)系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網(wǎng)安備42018502000812號