【題目】已知tanα=2．
（1）求 
的值；
（2）若α∈（0， 
），求sin（α﹣ 
）的值．
【答案】
（1）解：由tanα=2 知，cosα≠0，∴ 
= 
= 
（2）解：由tanα=2= 
，得sinα=2cosα，再根據sin2α+cos2α=1，α∈（0， 
），
求得cosα= 
，sinα= 
，
∴sin（α﹣ 
）=sinαcos ﹣cosαsin = 
﹣ 
= 
【解析】（1）利用同角三角函數的基本關系，求得要求式子的值．（2）利用同角三角函數的基本關系求得cosα 和sinα的值，再利用兩角差的正弦公式求得sin（α﹣ ）的值．
【考點精析】通過靈活運用同角三角函數基本關系的運用和兩角和與差的余弦公式，掌握同角三角函數的基本關系：
；
;（3） 倒數關系：
；兩角和與差的余弦公式：
即可以解答此題．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】如圖，已知在四棱錐P﹣ABCD中，底面ABCD是平行四邊形，PA⊥平面ABCD，PA= 
，AB=1．AD=2．∠BAD=120°，E，F，G，H分別是BC，PB，PC，AD的中點．
（Ⅰ）求證：PH∥平面GED；
（Ⅱ）過點F作平面α，使ED∥平面α，當平面α⊥平面EDG時，設PA與平面α交于點Q，求PQ的長．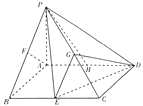
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】集合A={x|1≤x≤5}，B={x|2≤x≤6}，
（1）若x∈A，y∈B且均為整數，求x＞y的概率．
（2）若x∈A，y∈B且均為實數，求x＞y的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比，收獲時各隨機抽取了100個網箱，測量各箱水產品的產量（單位：kg）, 其頻率分布直方圖如下：
（1）記A表示事件“舊養殖法的箱產量低于50 kg”，估計A的概率；
（2）填寫下面列聯表，并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關：
箱產量＜50 kg | 箱產量≥50 kg | |
舊養殖法 | ||
新養殖法 |
（3）根據箱產量的頻率分布直方圖，對這兩種養殖方法的優劣進行比較.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）= 
x3﹣2ax2﹣3x（a∈R）． （Ⅰ）若f（x）在區間（﹣1，1）內為減函數，求實數a的取值范圍；
（Ⅱ）對于實數a的不同取值，試討論y=f（x）在（﹣1，1）內的極值點的個數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，曲線
在點
處的切線與直線
垂直（其中
為自然對數的底數）．
（I）求
的解析式及單調遞減區間；
（II）是否存在常數
，使得對于定義域內的任意
恒成立？若存在，求出
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨機詢問某大學40名不同性別的大學生在購買食物時是否讀營養說明，得到如下列聯表：
男 | 女 | 總計 | |
讀營養說明 | 16 | 8 | 24 |
不讀營養說明 | 4 | 12 | 16 |
總計 | 20 | 20 | 40 |
（1）根據以上列聯表進行獨立性檢驗，能否在犯錯誤的概率不超過0.01的前提下認為性別與是否讀營養說明之間有關系？
（2）從被詢問的16名不讀營養說明的大學生中，隨機抽取2名學生，求抽到男生人數
的分布列及其均值（即數學期望）．
（注： 
，其中
為樣本容量）
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
