日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
橢圓上一點，F1，F2為橢圓的左右焦點，若∠PF1F2=60°，∠PF2F1=30°，則此橢圓的離心率為（　　）
分析：利用含30°直角三角形的邊角關系、橢圓的定義、離心率計算公式即可得出．
解答：解：∵∠PF1F2=60°，∠PF2F1=30°，∴∠F1PF2=90°．
在Rt△PF1F2中，|PF2|=
1
2
|F1F2|=c，|PF1|=
3
c．
∵|PF1|+|PF2|=2a，
∴c+
3
c=2a，
∴e=
c
a
=
2
3
+1
=
3
-1．
故選B．
點評：本題考查了含30°直角三角形的邊角關系、橢圓的定義、離心率計算公式，屬于基礎題．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

精英家教網已知橢圓C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦點分別為F1、F2，P是橢圓上一點，且∠F1PF2=60°，設
|PF1|
|PF2|
=λ
（1）求橢圓C的離心率e和λ的函數關系式e=f（λ）
（2）若橢圓C的離心率e最小，且橢圓C上的動點M到定點N(0，
1
2
)的最遠距離為
5
，求橢圓C的方程．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知橢圓C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左，右焦點分別為F1，F2，其中F2也是拋物線C2：y2=4x的焦點，M是C1與C2在第一象限的交點，且MF2=
5
3
．
（1）求橢圓C1的方程；
（2）已知點A（1，m）（m＞0）是橢圓C1上一點，E，F是橢圓C1上的兩個動點，若直線AE的斜率與AF的斜率互為相反數，探求直線EF的斜率是否為定值？如果是，求出定值；反之，請說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2010•崇明縣二模）設橢圓
x2
a2
+
y2
b2
=1（a＞b＞0）與雙曲線
x2
3
-
y2
1
=1有相同的焦點F1（-c，0），F2（c，0）（c＞0），P為橢圓上一點，△PF1F2的最大面積等于2
2
．過點N（-3，0）且傾角為30°的直線l交橢圓于A、
B兩點．
（1）求橢圓的標準方程；
（2）求證：點F1（-c，0）在以線段AB為直徑的圓上；
（3）設E、F是直線l上的不同兩點，以線段EF為直徑的圓過點F1（-c，0），求|EF|的最小值并求出對應的圓方程．

查看答案和解析>>

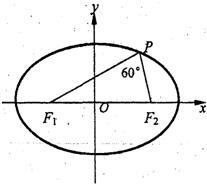
科目：高中數學 來源：2010-2011學年廣東省廣州市荔灣區廣雅中學高三（上）12月月考數學試卷（理科）（解析版） 題型：解答題

已知橢圓的左、右焦點分別為F1、F2，P是橢圓上一點，且∠F1PF2=60°，設
（1）求橢圓C的離心率e和λ的函數關系式e=f（λ）
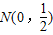（2）若橢圓C的離心率e最小，且橢圓C上的動點M到定點的最遠距離為，求橢圓C的方程．

查看答案和解析>>

科目：高中數學 來源：2010年上海市崇明縣高考數學二模試卷（文科）（解析版） 題型：解答題

設橢圓（a＞b＞0）與雙曲線有相同的焦點F1（-c，0），F2（c，0）（c＞0），P為橢圓上一點，△PF1F2的最大面積等于．過點N（-3，0）且傾角為30°的直線l交橢圓于A、
B兩點．
（1）求橢圓的標準方程；
（2）求證：點F1（-c，0）在以線段AB為直徑的圓上；
（3）設E、F是直線l上的不同兩點，以線段EF為直徑的圓過點F1（-c，0），求|EF|的最小值并求出對應的圓方程．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 色视频一区 | 国产精品三级 | 视频1区2区 | 四虎网址 | 精品一区国产 | 欧美日韩成人在线视频 | 久久伦理中文字幕 | 亚洲国产aⅴ成人精品无吗 91精品国产一区二区 | www.国产精品 | 91精品久久久久久久久 | 性处破╳╳╳高清欧美 | 99re6在线| 成人欧美一区二区三区 | 国产欧美精品一区aⅴ影院 日韩精品区 | 国产青草 | 日韩欧美一级在线 | 天堂一区二区三区在线 | 成人午夜电影网 | 成人国产在线观看 | 久久国产一区 | 亚洲在线成人 | 精品三级在线观看 | 午夜影院男女 | 国产精品久久久久aaaa | 亚洲动漫在线观看 | 欧美久久久久久久久中文字幕 | 久久久www成人免费精品 | 成人不卡一区二区 | 99精品网 | 国产日韩欧美精品一区 | 欧美在线a | 一区网站| 天天干天天操天天舔 | 免费特黄视频 | 黄a网| 久久男人天堂 | 欧美一区 | 久草在线资源福利站 | 日本亚洲欧美 | 黄色自拍视频 | 久久综合伊人 |