
(12)如圖,現在要在一塊半徑為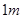 ,圓心角為
,圓心角為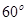 的扇形紙板
的扇形紙板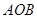 上剪出一個平行四邊形
上剪出一個平行四邊形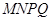 ,使點
,使點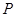 在弧
在弧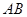 上,點
上,點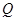 在
在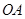 上,點
上,點 ,
, 在
在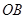 上,設
上,設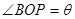 ,
,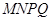 的面積為
的面積為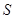 .
.
(1)求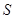 關于
關于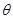 的函數關系式;
的函數關系式;
(2)求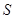 的最大值及相應
的最大值及相應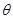 的值.
的值.
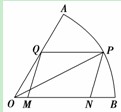
①分別過點P、Q作PD⊥OB,QE⊥OB,垂足分別為D、E,則四邊形QEDP是矩形.
PD=sinθ,OD=cosθ.
在Rt△OEQ中,∠AOB=,
則OE=QE=PD.
所以MN=PQ=DE=OD-OE=cosθ-sinθ.
則S=MN×PD=(cosθ-sinθ)×sinθ=sinθcosθ-sin2θ,θ∈(0,).
(2)S=sin2θ-(1-cos2θ)=sin2θ+cos2θ-=sin(2θ+)-.
因為0<θ<,所以<2θ+<,
所以<sin(2θ+)≤1. 所以當2θ+=,即θ=時,S的值最大為 m2.
即S的最大值是 m2,相應θ的值是.
【解析】略


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源:設計必修四數學人教A版 人教A版 題型:044
煙筒上的正弦函數
煙筒彎頭是由兩個圓柱形的煙筒焊在一起做成的,現在要用長方形鐵皮做成一個直角煙筒彎頭(兩個圓柱呈垂直狀),如圖所示,若煙筒的直徑為12 cm,最短母線為6 cm,應將鐵皮如何剪裁,才能既省工又省料呢?

查看答案和解析>>
科目:高中數學 來源: 題型:
 (12)如圖,現在要在一塊半徑為
(12)如圖,現在要在一塊半徑為![]() ,圓心角為
,圓心角為![]() 的扇形紙板
的扇形紙板![]() 上剪出一個平行四邊形
上剪出一個平行四邊形![]() ,使點
,使點![]() 在弧
在弧![]() 上,點
上,點![]() 在
在![]() 上,點
上,點![]() ,
,![]() 在
在![]() 上,設
上,設![]() ,
,![]() 的面積為
的面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)求![]() 的最大值及相應
的最大值及相應![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分)如圖,現在要在一塊半徑為1 m,圓心角為60°的扇形紙板AOB上剪出一個平行四邊形MNPQ,使點P在弧AB上,點Q在OA上,點M,N在OB上,設∠BOP=θ,MNPQ的面積為S.
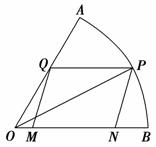 (1)求S關于θ的函數關系式;
(1)求S關于θ的函數關系式;
(2)求S的最大值及相應θ的值.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com