
【題目】某公司欲生產一款迎春工藝品回饋消費者,工藝品的平面設計如圖所示,該工藝品由直角![]() 和以
和以![]() 為直徑的半圓拼接而成,點
為直徑的半圓拼接而成,點![]() 為半圈上一點(異于
為半圈上一點(異于![]() ,
,![]() ),點
),點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() .已知
.已知![]() ,
,![]() ,設
,設![]() .
.

(1)為了使工藝禮品達到最佳觀賞效果,需滿足![]() ,且
,且![]() 達到最大.當
達到最大.當![]() 為何值時,工藝禮品達到最佳觀賞效果;
為何值時,工藝禮品達到最佳觀賞效果;
(2)為了工藝禮品達到最佳穩定性便于收藏,需滿足![]() ,且
,且![]() 達到最大.當
達到最大.當![]() 為何值時,
為何值時,![]() 取得最大值,并求該最大值.
取得最大值,并求該最大值.
科目:高中數學 來源: 題型:
【題目】(2016·北京卷)如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=![]() .
.
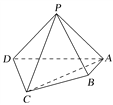
(1)求證:PD⊥平面PAB;
(2)求直線PB與平面PCD所成角的正弦值;
(3)在棱PA上是否存在點M,使得BM∥平面PCD?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廟會是我國古老的傳統民俗文化活動,又稱“廟市”或 “節場”.廟會大多在春節、元宵節等節日舉行.廟會上有豐富多彩的文化娛樂活動,如“砸金蛋”(游玩者每次砸碎一顆金蛋,如果有獎品,則“中獎”).今年春節期間,某校甲、乙、丙、丁四位同學相約來到某廟會,每人均獲得砸一顆金蛋的機會.游戲開始前,甲、乙、丙、丁四位同學對游戲中獎結果進行了預測,預測結果如下:
甲說:“我或乙能中獎”; 乙說:“丁能中獎”;
丙說:“我或乙能中獎”; 丁說:“甲不能中獎”.
游戲結束后,這四位同學中只有一位同學中獎,且只有一位同學的預測結果是正確的,則中獎的同學是( )

A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高三年級某班50名學生期中考試數學成績的頻率分布直方圖如圖所示,成績分組區間為:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中
.其中![]() 成等差數列且
成等差數列且![]() .
.
物理成績統計如表.(說明:數學滿分150分,物理滿分100分)

分組 |
|
|
|
|
|
頻數 | 6 | 9 | 20 | 10 | 5 |
(1)根據頻率分布直方圖,請估計數學成績的平均分;
(2)若數學成績不低于140分的為“優”,物理成績不低于90分的為“優”,已知本班中至少有一個“優”的同學總數為6人,從數學成績為“優”的同學中隨機抽取2人,求兩人恰好均為物理成績“優”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區高考實行新方案,規定:語文、數學和英語是考生的必考科目,考生還須從物理、化學、生物、歷史、地理和政治六個科目中選取三個科目作為選考科目,若一名學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定.例如,學生甲選擇“物理、化學和生物”三個選考科目,則學生甲的選考方案確定,“物理、化學和生物”為其選考方案.
某學校為了了解高一年級420名學生選考科目的意向,隨機選取30名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
選考方案待確定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 選考方案確定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
選考方案待確定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估計該學校高一年級選考方案確定的學生中選考生物的學生有多少人?
(Ⅱ)假設男生、女生選擇選考科目是相互獨立的.從選考方案確定的8位男生隨機選出1人,從選考方案確定的10位女生中隨機選出1人,試求該男生和該女生的選考方案中都含有歷史科目的概率;
(Ⅲ)從選考方案確定的8名男生隨機選出2名,設隨機變量兩名男生選考方案相同時![]() ,兩名男生選考方案不同時
,兩名男生選考方案不同時![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過橢圓![]() 的左焦點的直線
的左焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 過坐標原點且與直線
過坐標原點且與直線![]() 的斜率互為相反數.若直線
的斜率互為相反數.若直線![]() 與橢圓交于
與橢圓交于![]() 兩點且均不與點
兩點且均不與點![]() 重合,設直線
重合,設直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,直線
,直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,判斷
,判斷![]() 與
與![]() 的大小關系并加以證明.
的大小關系并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于![]() 若數列
若數列![]() 滿足
滿足![]() 則稱這個數列為“
則稱這個數列為“![]() 數列”.
數列”.
(Ⅰ)已知數列1, ![]() 是“
是“![]() 數列”,求實數
數列”,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)是否存在首項為![]() 的等差數列
的等差數列![]() 為“
為“![]() 數列”,且其前
數列”,且其前![]() 項和
項和![]() 使得
使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的通項公式;若不存在,請說明理由;
的通項公式;若不存在,請說明理由;
(Ⅲ)已知各項均為正整數的等比數列![]() 是“
是“![]() 數列”,數列
數列”,數列![]() 不是“
不是“![]() 數列”,若
數列”,若![]() 試判斷數列
試判斷數列![]() 是否為“
是否為“![]() 數列”,并說明理由.
數列”,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
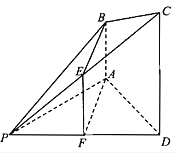
【題目】四棱錐![]() 中,已知
中,已知![]() 平面PAD,
平面PAD,![]() ,
,![]() ,E為棱PC上的一點,經過A,B,E三點的平面與棱PD相交于點F.
,E為棱PC上的一點,經過A,B,E三點的平面與棱PD相交于點F.
![]() 求證:
求證:![]() 平面PAD;
平面PAD;
![]() 求證:
求證:![]() ;
;
![]() 若平面
若平面![]() 平面PCD,求證:
平面PCD,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com