
定義區間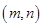 ,
,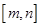 ,
,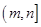 ,
,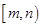 的長度均為
的長度均為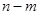 ,其中
,其中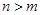 .
.
(1)求關于 的不等式
的不等式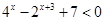 的解集構成的區間的長度;
的解集構成的區間的長度;
(2)若關于 的不等式
的不等式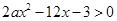 的解集構成的區間的長度為
的解集構成的區間的長度為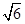 ,求實數
,求實數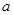 的值;
的值;
(3)已知關于 的不等式
的不等式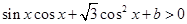 ,
,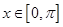 的解集構成的各區間的長度和超過
的解集構成的各區間的長度和超過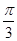 ,求實數
,求實數 的取值范圍.
的取值范圍.
(1)區間的長度是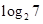 .
.
(2)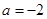 (
(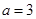 舍).
舍).
(3)實數 的取值范圍是
的取值范圍是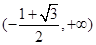 .
.
解析試題分析:(1)不等式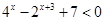 的解是
的解是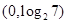
所以區間的長度是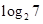 3分
3分
(2)
當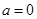 時,不符合題意 4分
時,不符合題意 4分
當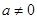 時,
時,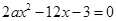 的兩根設為
的兩根設為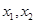 ,且
,且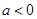
結合韋達定理知 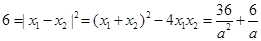
解得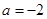 (
(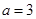 舍) 7分
舍) 7分
(3)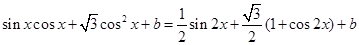
=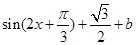
設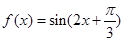 ,原不等式等價于
,原不等式等價于  ,
, 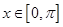 9分
9分
因為函數 的最小正周期是
的最小正周期是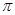 ,
,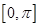 長度恰為函數的一個正周期
長度恰為函數的一個正周期
所以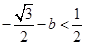 時,
時, ,
, 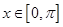 的解集構成的各區間的長度和超過
的解集構成的各區間的長度和超過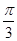
即實數 的取值范圍是
的取值范圍是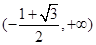 12分
12分
考點:指數不等式,和差倍半的三角函數公式,三角不等式,三角函數圖象和性質。
點評:難題,指數不等式,常常化為同底數指數冪的不等關系或利用“換元法”,加以轉化。三角函數不等式問題,通常利用三角公式進行化簡,結合三角函數的圖象和性質,加以處理,本題較難。


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com