
△ABC的角A、B、C的對邊分別為a、b、c,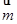 =(2b-c,a),
=(2b-c,a),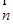 =(cosA,-cosC),且
=(cosA,-cosC),且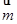 ⊥
⊥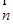 .
.
(Ⅰ)求角A的大小;
(Ⅱ)當y=2sin2B+sin(2B+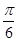 )取最大值時,求角
)取最大值時,求角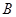 的大小.
的大小.
(Ⅰ) A=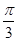 .(Ⅱ) B=
.(Ⅱ) B=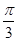 時,y取最大值2.
時,y取最大值2.
【解析】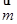 ⊥
⊥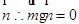 .考查數量積的坐標表示,
.考查數量積的坐標表示,
,求y=2sin2B+sin(2B+ )取最大值時,將函數解析式化為y=1+sin(2B-
)取最大值時,將函數解析式化為y=1+sin(2B- ).
).
然后作用的角用整體法- <2B-
<2B- <
<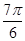 ,在范圍內求最值。
,在范圍內求最值。
解: (Ⅰ)由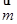 ⊥
⊥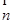 ,得
,得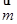 ·
·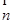 =0,從而(2b-c)cosA-acosC=0,
=0,從而(2b-c)cosA-acosC=0,
由正弦定理得2sinBcosA-sinCcosA-sinAcosC=0
∴2sinBcosA-sin(A+C)=0,2sinBcosA-sinB=0,
∵A、B∈(0,π),∴sinB≠0,cosA=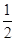 ,故A=
,故A=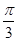 .……………………6分
.……………………6分
(Ⅱ)y=2sin2B+2sin(2B+ )=(1-cos2B)+sin2Bcos
)=(1-cos2B)+sin2Bcos +cos2Bsin
+cos2Bsin
=1+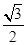 sin2B-
sin2B-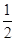 cos2B=1+sin(2B-
cos2B=1+sin(2B- ).
).
由(Ⅰ)得,0<B<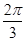 ,-
,- <2B-
<2B- <
<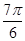 ,
,
∴當2B- =
=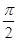 ,即B=
,即B=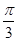 時,y取最大值2
時,y取最大值2


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 3 |
| m |
| n |
| p |
| m |
| n |
| m |
| p |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com