
【題目】已知焦點在x軸上且長軸長為4的橢圓C過點T(1,1),記l為圓O:x2+y2=1的切線
(1)求橢圓C的方程;
(2)若l與橢圓C交于A、B兩點,求證:∠AOB為定值.
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱錐![]() 的三條側棱
的三條側棱![]() ,
, ![]() ,
, ![]() 兩兩垂直,
兩兩垂直, ![]() 為等邊三角形,
為等邊三角形, ![]() 為
為![]() 內部一點,點
內部一點,點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .
.
(Ⅰ)證明: ![]() ;
;
(Ⅱ)證明: ![]() ;
;
(Ⅲ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 共有k
共有k![]() 項,且同時滿足
項,且同時滿足![]() ,
,![]() ,則稱數列
,則稱數列![]() 為
為![]() 數列.
數列.
(1)若等比數列![]() 為
為![]() 數列,求
數列,求![]() 的值;
的值;
(2)已知![]() 為給定的正整數,且
為給定的正整數,且![]() ,
,
①若公差為![]()
![]() 的等差數列
的等差數列![]() 是
是![]() 數列,求公差d;
數列,求公差d;
②若數列![]() 的通項公式為
的通項公式為
![]() ,其中常數
,其中常數![]() ,判斷數列
,判斷數列![]() 是否為
是否為![]() 數列,并說明理由.
數列,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】治理大氣污染刻不容緩,根據我國分布的《環(huán)境空氣質量數(AQI)技術規(guī)定》:空氣質量指數劃分階為0~50、51~100、101~150、151~200、201~300和大于300六級,對應于空氣質量指數的六個級別,指數越大,級別越高,說明污染越嚴重,對人體健康的影響也越明顯.專家建議:當空氣質量指數小于![]() 時,可以戶外運動;空氣質量指數
時,可以戶外運動;空氣質量指數![]() 及以上,不適合進行旅游等戶外活動,以下是某市
及以上,不適合進行旅游等戶外活動,以下是某市![]() 年
年![]() 月中旬的空氣質量指數情況:
月中旬的空氣質量指數情況:
時間 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(1)求![]() 月中旬市民不適合進行戶外活動的概率;
月中旬市民不適合進行戶外活動的概率;
(2)一外地游客在![]() 月中旬來該市旅游,想連續(xù)游玩兩天,求適合旅游的概率.
月中旬來該市旅游,想連續(xù)游玩兩天,求適合旅游的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 過點
過點![]() ,且傾斜角為
,且傾斜角為![]() ,以坐標原點為極點,
,以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,圓
軸的正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的直角坐標方程及直線
的直角坐標方程及直線![]() 的參數方程;
的參數方程;
(2)設直線![]() 與圓
與圓![]() 的兩個交點分別為
的兩個交點分別為![]() ,
, ![]() ,求證:
,求證: 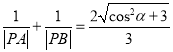 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學的環(huán)保社團參照國家環(huán)境標準制定了該校所在區(qū)域空氣質量指數與空氣質量等級對應關系如下表(假設該區(qū)域空氣質量指數不會超過300):
空氣質量指數 |
|
|
|
|
|
|
空氣質量等級 | 1級優(yōu) | 2級良 | 3級輕度污染 | 4級中度污染 | 5級重度污染 | 6級嚴重污染 |
該社團將該校區(qū)在2018年11月中10天的空氣質量指數監(jiān)測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.

(Ⅰ)以這10天的空氣質量指數監(jiān)測數據作為估計2018年11月的空氣質量情況,則2018年11月中有多少天的空氣質量達到優(yōu)良?
(Ⅱ)已知空氣質量等級為1級時不需要凈化空氣,空氣質量等級為2級時每天需凈化空氣的費用為1000元,空氣質量等量等級為3級時每天需凈化空氣的費用為2000元.若從這10天樣本中空氣質量為1級、2級、3級的天數中任意抽取兩天,求這兩天的凈化空氣總費用為3000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn,若S9=81,a3+a5=14.
(1)求數列{an}的通項公式;
(2)設bn=![]() ,若{bn}的前n項和為Tn,證明:Tn<
,若{bn}的前n項和為Tn,證明:Tn<![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com