
(Ⅰ)設{an}是集合![]() 中所有的數從小到大排列成的數列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
中所有的數從小到大排列成的數列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,……
將數列{an}各項按照上小下大,左小右大的原則寫成如下的三角形數表:
(i)寫出這個三角形數表的第四行、第五行各數;
(ii)求a100.
(Ⅱ)(本小題為附加題,如果解答正確,加4分,但全卷總分不超過150分)
設{bn}是集合![]() 中所有的數從小到大排列成的數列,已知bk =1160,求k.
中所有的數從小到大排列成的數列,已知bk =1160,求k.
(Ⅰ)解:(i)第四行 17 18 20 24
第五行 33 34 36 40 48
(ii)解法一:設![]() ,只須確定正整數t0,s0
,只須確定正整數t0,s0
數列{an}中小于![]() 的項構成的子集為
的項構成的子集為![]() ,
,
其元素個數為 ![]()
依題意 ![]()
滿足上式的最大整數t0為14,所以取t0=14.
因為![]() ,由此解得s0=8.∴ a 100=214+28=16640.
,由此解得s0=8.∴ a 100=214+28=16640.
解法二:n為an的下標.
三角形數表第一行第一個元下標為1.
第二行第一個元下標為![]()
……
第t行第一個元下標為![]() 第t行第s個元下標為
第t行第s個元下標為![]() 該元等于2t+2t-1.
該元等于2t+2t-1.
據此判斷a100所在的行.
因為![]() ,所以a100是三角形表第14行的第9個元
,所以a100是三角形表第14行的第9個元
a100=214+29-1=16640.
(Ⅱ)(本小題為附加題,如果解答正確,加4分,但全卷總分不超過150分)
解:bk=1160=210+27+23.
令 M={c∈B | c <1160} (其中,B=![]() ).
).
因M={c∈B | c <210}∪{c∈B | 210 < c<210+27} ∪{c∈B | 210+27< c<210+27+23}.
現在求M的元素個數: {c∈B | c <210}=![]() ,
,
其元素個數為![]() ; {c∈B | 210 < c <210+27}={210+2s+2r | 0≤r<s<7}
; {c∈B | 210 < c <210+27}={210+2s+2r | 0≤r<s<7}
其元素個數為![]() ; {c∈B | 210+27 < c <210+27+23 }={210+27+2r | 0≤r<3},
; {c∈B | 210+27 < c <210+27+23 }={210+27+2r | 0≤r<3},
其元素個數為![]() .
.


科目:高中數學 來源: 題型:
g(
| ||
| dn+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
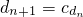 (n∈N*).求數列{dn}的通項公式;
(n∈N*).求數列{dn}的通項公式;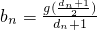 ,試判斷數列{bn}是否為等差數列,并說明理由.
,試判斷數列{bn}是否為等差數列,并說明理由.查看答案和解析>>
科目:高中數學 來源:朝陽區二模 題型:解答題
g(
| ||
| dn+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)求Sn;
(2)設cn=an+8n+3,數列{dn}滿足d1=c1,dn+1=![]() (n∈N*),求數列{dn}的通項公式;
(n∈N*),求數列{dn}的通項公式;
(3)設g(x)是定義在正整數集上的函數,對于任意的正整數x1、x2,恒有g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a(a為常數,且a≠0),記bn= ,試判斷數列{bn}是否為等差數列,并說明理由.
,試判斷數列{bn}是否為等差數列,并說明理由.
查看答案和解析>>
科目:高中數學 來源:2008年北京市朝陽區高考數學二模試卷(文科)(解析版) 題型:解答題
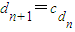 (n∈N*).求數列{dn}的通項公式;
(n∈N*).求數列{dn}的通項公式;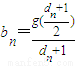 ,試判斷數列{bn}是否為等差數列,并說明理由.
,試判斷數列{bn}是否為等差數列,并說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com