
【題目】當![]() ,則稱點
,則稱點![]() 為平面上單調格點:設
為平面上單調格點:設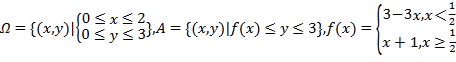
求從區域![]() 中任取一點
中任取一點![]() ,而該點落在區域
,而該點落在區域![]() 上的概率;
上的概率;
求從區域![]() 中的所有格點中任取一點
中的所有格點中任取一點![]() ,而該點是區域
,而該點是區域![]() 上的格點的概率.
上的格點的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)作出集合![]() 所對應的區域,記事件
所對應的區域,記事件![]() “從區域
“從區域![]() 中任取一點
中任取一點![]() ,而該點落在區域
,而該點落在區域![]() 上”,根據幾何概型,利用面積比,即可求解概率;
上”,根據幾何概型,利用面積比,即可求解概率;
(2)事件![]() “從區域
“從區域![]() 中的所有格點中任取一點
中的所有格點中任取一點![]() ,而該點是區域
,而該點是區域![]() 上的格點”,得出基本事件的總數,和事件
上的格點”,得出基本事件的總數,和事件![]() 所包含的基本事件的個數,利用古典概型及概率的計算公式,即可求解事件的概率.
所包含的基本事件的個數,利用古典概型及概率的計算公式,即可求解事件的概率.
試題解析:
作出集合![]() 所對應的區域(如圖):
所對應的區域(如圖):
矩形![]()
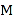
則:(1)記事件![]() “從區域
“從區域![]() 中任取一點
中任取一點![]() ,而該點落在區域
,而該點落在區域![]() 上”
上”
則事件![]() 符合幾何概型,即
符合幾何概型,即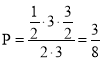 .
.
(2)事件![]() “從區域
“從區域![]() 中的所有格點中任取一點
中的所有格點中任取一點![]() ,而該點是區域
,而該點是區域![]() 上的格點”
上的格點”
則事件![]() 符合古典概型,區域
符合古典概型,區域![]() 中的格點個數:當橫坐標分別為0,1,2時,縱坐標可以為0,1,2,3中的任一個,此時有
中的格點個數:當橫坐標分別為0,1,2時,縱坐標可以為0,1,2,3中的任一個,此時有![]() 個;而區域
個;而區域![]() 上的格點有(0,3),(1,2),(2,3),(1,2)共4個,
上的格點有(0,3),(1,2),(2,3),(1,2)共4個,
∴![]()


科目:高中數學 來源: 題型:
【題目】已知△ABC中,A,B,C的對邊分別是a,b,c,且2cos2 ![]() sinB,a=3c
sinB,a=3c
(Ⅰ)分別求tanC和sin2C的值;
(Ⅱ)若b=1,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}的前n項和Sn , 首項a1=a,公比為q(q≠0且q≠1).
(1)推導證明:Sn= ![]() ;
;
(2)等比數列{an}中,是否存在連續的三項:ak、ak+1、ak+2 , 使得這三項成等差數列?若存在,求出符合條件的等比數列公比q的值,若不存在,說明理由;
(3)本題中,若a=q=2,已知數列{nan}的前n項和Tn , 是否存在正整數n,使得Tn≥2016?若存在,求出n的取值集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的角A、B、C所對的邊分別是a、b、c,設向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求證:△ABC為等腰三角形;
,求證:△ABC為等腰三角形;
(2)若 ![]() ⊥
⊥ ![]() ,邊長c=2,角C=
,邊長c=2,角C= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校用簡單隨機抽樣方法抽取了30名同學,對其每月平均課外閱讀時間(單位:小時)進行調查,莖葉圖如圖:
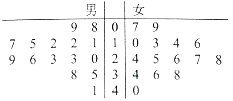
若將月均課外閱讀時間不低于30小時的學生稱為“讀書迷”.
(1)將頻率視為概率,估計該校900名學生中“讀書迷”有多少人?
(2)從已抽取的7名“讀書迷”中隨機抽取男、女“讀書迷”各1人,參加讀書日宣傳活動.
(i)共有多少種不同的抽取方法?
(ii)求抽取的男、女兩位“讀書迷”月均讀書時間相差不超過2小時的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com