Question

（本題滿分15分）

    已知函數在x=±1處取得極值

（1）求函數的解析式；

（2）求證：對于區間[－1，1]上任意兩個自變量的值x1，x2，都有≤4；

（3）若過點A（1，m）（m ≠－2）可作曲線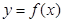的三條切線，求實數m的范圍。

 

Answer 1

【答案】

 

（1）f(x)=x3－3x

（2）略

（3－3<m<－2）

【解析】解：   （1）=3ax2+2bx－3，依題意，f′(1)=f′(－1)=0，

        即             …………………   2分

        解得a=1，b=0.

        ∴f(x)=x3－3x.           ………………………    4分

   （2）∵f(x)=x3－3x,∴f ′(x)=3x2－3=3(x+1)(x－1)，

當－1<x<1時，f ′ (x)<0，故f(x)在區間[－1，1]上為減函數，

fmax(x)=f(－1)=2，fmin(x)=f(1)=－2    ……………………   6分

∵對于區間[－1，1]上任意兩個自變量的值x1，x2，

都有|f(x1)－f(x2)|≤|fmax(x) －fmin(x)|

|f(x1)-f(x2)|≤|fmax(x)-fmin(x)|=2-(－2)=4     ………………  8分

   （3）f′(x)=3x2－3=3(x+1)(x－1)，

         ∵曲線方程為y=x3－3x，∴點A（1，m）不在曲線上.

設切點為M（x0，y0），則點M的坐標滿足

因，故切線的斜率為，

整理得.

∵過點A（1，m）可作曲線的三條切線，

∴關于x₀方程=0有三個實根.   ………………  11分

設g(x­₀)= ，則g′(x0)=6，

由g′(x₀)=0，得x0=0或x0­=1.

∴g(x0)在（－∞，0），（1，+∞）上單調遞增，在（0，1）上單調遞減.

∴函數g(x0)= 的極值點為x0=0，x0=1  …………… 13分

∴關于x0方程=0有三個實根的充要條件是

，解得－3<m<－2.

故所求的實數a的取值范圍是－3<m<－2.   ……………  15分