
分析:本題考查常見函數的導數及用導數求最值等知識點.求函數最值的關鍵是選好自變量建立目標函數.一般說來,若f(x)是關于x的二次函數,可用配方法,也可用求導的方法求最值;若f(x)是三次或三次以上函數,則用求導的方法求最值,但均需注意函數的定義域.
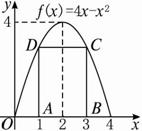
解:如上圖,f(x)=4x-x2=-(x-2)2+4,它的對稱軸方程是x=2,頂點坐標是(2,4).
不妨設A(x,0)(0<x<2),則B(4-x,0),D(x,f(x)).
∵D(x,f(x))在拋物線上,∴f(x)=4x-x2.
∴S矩形ABCD=(4-2x)(4x-x2)
=2x3-12x2+16x(0<x<2).
∴S′=6x2-24x+16.
令S′=0,得x1=2-![]() ,x2=2+
,x2=2+![]() (舍去).
(舍去).
又∵S矩形ABCD在x∈(0,2)上只有一個極值點,
∴它必是一個最值點.
∴[S矩形ABCD]max=2(2-![]() )3-12(2-
)3-12(2-![]() )2+16(2-
)2+16(2-![]() )=
)=![]() .
.


科目:高中數學 來源:導學大課堂選修數學1-1蘇教版 蘇教版 題型:044
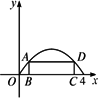
如圖,在二次函數f(x)=4x-x2的圖象與x軸所圍成的圖形中,有一矩形ABCD,求這個矩形ABCD的最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
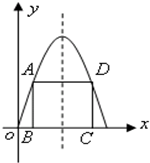 如圖,在二次函數f(x)=4x-x2的圖象與x軸所圍成的圖形中有一個內接矩形ABCD,設點B(x,0),則x=________,矩形面積最大.
如圖,在二次函數f(x)=4x-x2的圖象與x軸所圍成的圖形中有一個內接矩形ABCD,設點B(x,0),則x=________,矩形面積最大.查看答案和解析>>
科目:高中數學 來源:2009-2010學年浙江省臺州中學高二(上)第二次統練數學試卷(文科)(解析版) 題型:填空題
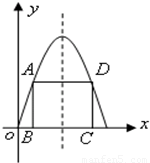
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com