Question

如圖，點D，E，F分別是四面體S－ABC的棱CA，CB，CS的中點，過點C作一直線分別交AB，DE于點G，H，連接SG，FH．

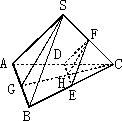
求證：SG∥FH．

Answer 1

答案：
解析：

分析：觀察圖形，易判定平面FDE∥平面SAB，而SG，FH是第三個平面SGC與上述兩個平行平面的交線，于是要證SG∥FH，可利用面面平行的性質定理． 　　證明：由題意知，EF為△SBC的中位線， 　　所以EF∥BS． 　　因為EF平面SAB，SB平面SAB， 　　所以EF∥平面SAB． 　　同理可得DF∥平面SAB． 　　又EF∩DF＝F， 　　所以平面DEF∥平面SAB． 　　又平面SGC∩平面SAB＝SG，平面SGC∩平面DEF＝FH， 　　由平面與平面平行的性質定理，得SG∥FH． 　　點評：應用面面平行的性質定理證明線線平行的關鍵是：先找到兩個平行平面(有時需證明)，再找第三個與它們相交的平面．而第三個平面與兩個平行平面的交線就是需要證明的兩平行線，于是，由面面平行推知線線平行． 　　解決空間平行問題最根本的是學會轉化，此外需要平面幾何知識作基礎．同學們在學習中要善于思考和總結，這樣，才能提高自己的解題能力．