數列
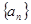
前
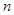
項和
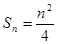
,數列
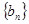
滿足
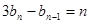
(
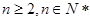
),
(1)求數列
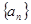
的通項公式;
(2)求證:當
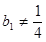
時,數列
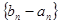
為等比數列;
(3)在(2)的條件下,設數列
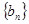
的前
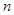
項和為
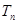
,若數列
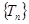
中只有
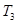
最小,求
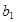
的取值范圍.
(1)
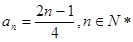
;(2)詳見解析;(3)
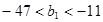
.
試題分析:(1)由
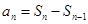
求解,注意
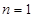
,若滿足則不用分段函數,若不滿足則
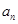
需要用分段函數表示;(2)要證明數列
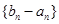
是等比數列,需要證明
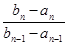
是常數,由條件只需要證明
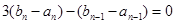
即可;(3)數列
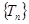
中只有
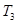
最小,可確定
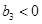
且
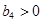
,再證明數列
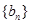
是遞增數列,從而可以確定
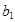
的取值范圍,.
試題解析:(1)

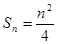
,
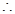
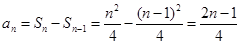
,
當
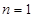
時
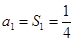
,也滿足,
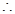
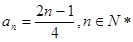
.
(2)

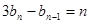
,
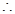
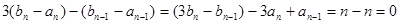
,
所以
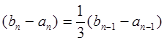
,且
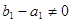
,
所以
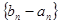
是以
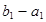
為首項、
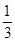
為公比的等比數列;
(3)
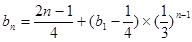
;
因為數列
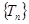
中只有
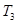
最小,所以
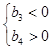
,解得
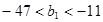
;
此時,
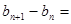
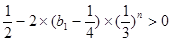
,于是,
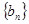
為遞增數列,
所以
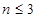
時
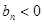
、
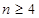
時
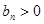
,符合題意,綜上
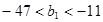
.
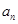
與
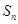
的關系,等比數列的性質,最值問題.
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
設無窮等比數列
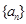
的公比為q,且
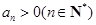
,
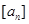
表示不超過實數
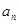
的最大整數(如
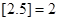
),記
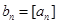
,數列
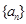
的前
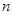
項和為
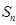
,數列
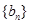
的前
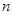
項和為
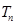
.
(Ⅰ)若
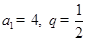
,求
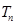
;
(Ⅱ)若對于任意不超過
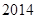
的正整數n,都有
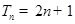
,證明:
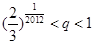
.
(Ⅲ)證明:
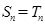
(
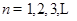
)的充分必要條件為
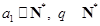
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知
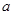
為實數,數列
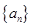
滿足
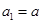
,當
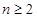
時,
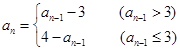
,
(Ⅰ)
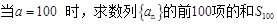
;(5分)
(Ⅱ)證明:對于數列
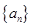
,一定存在
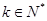
,使
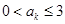
;(5分)
(Ⅲ)令
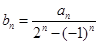
,當
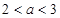
時,求證:
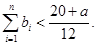
(6分)
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知
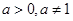
,數列
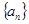
是首項為
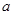
,公比也為
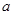
的等比數列,令
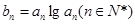
(Ⅰ)若
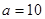
,求數列
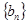
的前
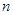
項和
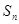
;
(Ⅱ)當數列
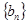
中的每一項總小于它后面的項時,求
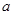
的取值范圍.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知各項均為正數的數列
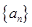
的前
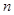
項和為
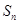
,數列
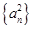
的前
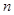
項和為
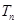
,且
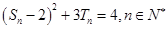
.
⑴證明:數列
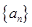
是等比數列,并寫出通項公式;
⑵若
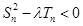
對
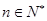
恒成立,求
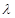
的最小值;
⑶若
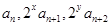
成等差數列,求正整數
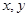
的值.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列
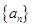
,滿足
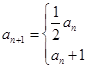
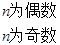
,
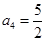
,若
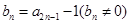
。
(1)求
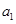
; (2)求證:
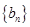
是等比數列; (3)若數列
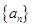
的前
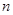
項和為
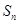
,求
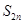
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列
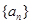
的前
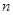
項和是
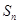
,且
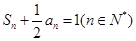
.
(1)求數列
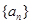
的通項公式;
(2)設
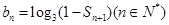
,求適合方程
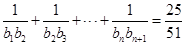
的正整數
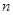
的值.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
已知正項等比數列{
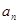
}的前n項和為
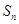
,且
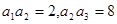
,則
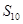
= __________.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
已知
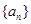
是公比為
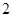
的等比數列,若
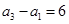
,則
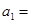
;
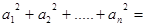
______________.
查看答案和解析>>
主站蜘蛛池模板:
欧美成人黑人xx视频免费观看
|
日本久久久久久
|
久久久青草婷婷精品综合日韩
|
国产亚洲精品一区二区
|
在线亚洲一区
|
欧美激情视频免费观看
|
亚洲乱码一区二区
|
日韩在线资源
|
精品亚洲一区二区三区
|
精品久久中文
|
91免费小视频
|
欧美日韩中文一区
|
日本好好热视频
|
激情久久av一区av二区av三区
|
国产精品久久国产精品
|
国产一区二区影院
|
啪啪小视频网站
|
国产91网址
|
日韩一区二区在线免费观看
|
亚洲最大成人
|
色美av|
国产精品久久久久久久久免费高清
|
亚洲欧美日韩精品
|
久久精品视频在线观看
|
逼逼av|
美女天天操
|
青青青久草
|
色网址在线|
久久无码精品一区二区三区
|
亚洲一区中文字幕在线观看
|
www.av7788.com|
国产精品毛片一区二区三区
|
亚洲一区二区三区在线播放
|
国产aaaaav久久久一区二区
|
亚洲综合第一页
|
segui88久久综合9999
|
久久久久国产一区
|
欧美 日韩 国产 一区
|
久久免费精品视频
|
欧洲一区二区三区
|
操到爽|

 前
前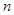 項和
項和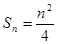 ,數列
,數列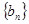 滿足
滿足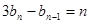 (
(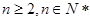 ),
),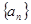 的通項公式;
的通項公式;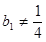 時,數列
時,數列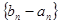 為等比數列;
為等比數列;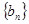 的前
的前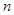 項和為
項和為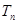 ,若數列
,若數列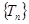 中只有
中只有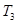 最小,求
最小,求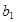 的取值范圍.
的取值范圍. 閱讀快車系列答案
閱讀快車系列答案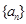 的公比為q,且
的公比為q,且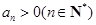 ,
,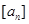 表示不超過實數
表示不超過實數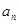 的最大整數(如
的最大整數(如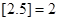 ),記
),記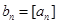 ,數列
,數列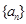 的前
的前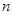 項和為
項和為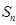 ,數列
,數列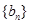 的前
的前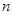 項和為
項和為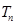 .
.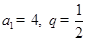 ,求
,求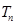 ;
;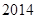 的正整數n,都有
的正整數n,都有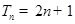 ,證明:
,證明: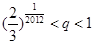 .
.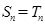 (
(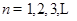 )的充分必要條件為
)的充分必要條件為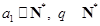 .
.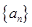 的前
的前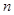 項和為
項和為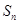 ,數列
,數列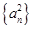 的前
的前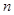 項和為
項和為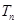 ,且
,且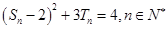 .
.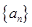 是等比數列,并寫出通項公式;
是等比數列,并寫出通項公式;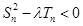 對
對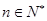 恒成立,求
恒成立,求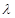 的最小值;
的最小值;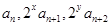 成等差數列,求正整數
成等差數列,求正整數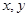 的值.
的值.