
���}Ŀ����֪�E�A![]() :
:![]() (
(![]() )���x���ʞ�
)���x���ʞ�![]() ���O(sh��)ֱ��(xi��n)
���O(sh��)ֱ��(xi��n)![]() �^(gu��)�E�A
�^(gu��)�E�A![]() ������c(di��n)������c(di��n)������(bi��o)ԭ�c(di��n)
������c(di��n)������c(di��n)������(bi��o)ԭ�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x��
�ľ��x��![]() .
.
��1����E�A![]() �ķ���.
�ķ���.
��2���^(gu��)�c(di��n)![]() ��б�ʲ������ֱ��(xi��n)
��б�ʲ������ֱ��(xi��n)![]() ���E�A
���E�A![]() ��
��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() �S�������S���Ƿ���ڶ��c(di��n)
�S�������S���Ƿ���ڶ��c(di��n)![]() ��ʹ��ֱ��(xi��n)
��ʹ��ֱ��(xi��n)![]() ��
��![]() ��б��֮�e�����ij���(sh��)?�����ڣ�������c(di��n)
��б��֮�e�����ij���(sh��)?�����ڣ�������c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
���𰸡���1��![]() ��2�����ڣ�
��2�����ڣ�![]()
��������
��1���O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() �����x���ʺ�ԭ�c(di��n)
�����x���ʺ�ԭ�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x��
�ľ��x��![]() ���ɵ��P(gu��n)��
���ɵ��P(gu��n)��![]() �ķ��̽M���ⷽ�̽M��
�ķ��̽M���ⷽ�̽M��![]() ���ɵô𰸣�
���ɵô𰸣�
��2�����}����O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() ��
��![]() ��ֱ��(xi��n)���̴�������(xi��n)���̣������Єeʽ����0��
��ֱ��(xi��n)���̴�������(xi��n)���̣������Єeʽ����0��![]() �ķ����������f�_(d��)�����ɵ�
�ķ����������f�_(d��)�����ɵ�![]() �c
�c![]() ���P(gu��n)ϵ�������O(sh��)�����c(di��n)
���P(gu��n)ϵ�������O(sh��)�����c(di��n)
![]() ʹ���}����������б�ʹ�ʽ��������(bi��o)�M(j��n)��Ӌ(j��)�㣬����(w��n)�}�D(zhu��n)����������(w��n)�}�����ɵô�.
ʹ���}����������б�ʹ�ʽ��������(bi��o)�M(j��n)��Ӌ(j��)�㣬����(w��n)�}�D(zhu��n)����������(w��n)�}�����ɵô�.
��1���O(sh��)�E�A�뽹����![]() .����(j��)�}��ã��E�A�x����
.����(j��)�}���E�A�x����![]() ����
����![]() ��
��
����![]() .��
.��
��?y��n)�ֱ��(xi��n)![]() �^(gu��)�E�A
�^(gu��)�E�A![]() ������c(di��n)������c(di��n)��
������c(di��n)������c(di��n)��
�����O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() .
.
�����c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ľ��x��
�ľ��x��![]() ����
����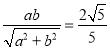 .��
.��
(li��n)���٢ڽ��![]() ��
��![]() .���ԙE�A
.���ԙE�A![]() �ķ��̞�
�ķ��̞�![]() .
.
��2�����}����O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() ��
��![]() .(li��n)��
.(li��n)��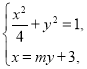 ��
��![]() .����
.����![]() ������
������![]() .
.
����![]() ��
��![]() ��
��
�t![]() ��
��![]() .
.
���O(sh��)���ڶ��c(di��n)![]() (
(![]() )��ʹ��ֱ��(xi��n)
)��ʹ��ֱ��(xi��n)![]() ��
��![]() ��б��֮�e����㳣��(sh��)��
��б��֮�e����㳣��(sh��)��
����![]()
![]()
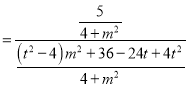
![]() .
.
Ҫʹ![]() ����㳣��(sh��)����(d��ng)�҃H��(d��ng)
����㳣��(sh��)����(d��ng)�҃H��(d��ng)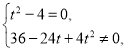 ���
���![]() (ؓ(f��)ֵ��ȥ).
(ؓ(f��)ֵ��ȥ).
��(d��ng)![]() �r(sh��)������(sh��)��
�r(sh��)������(sh��)��![]() .
.
����![]() �S�������S�ϴ��ڶ��c(di��n)
�S�������S�ϴ��ڶ��c(di��n)![]() ��ʹ��ֱ��(xi��n)
��ʹ��ֱ��(xi��n)![]() ��
��![]() ��б��֮�e�鳣��(sh��)
��б��֮�e�鳣��(sh��)![]() .
.


 ��x��܇(ch��)ϵ�д�
��x��܇(ch��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)![]() ���p����(xi��n)
���p����(xi��n)![]()
![]() ��
��![]() ��
��![]() ���ϣ����p����(xi��n)��һ�l�u����(xi��n)�ķ�����
���ϣ����p����(xi��n)��һ�l�u����(xi��n)�ķ�����![]() ��
��
��1�����p����(xi��n)![]() �ķ��̣�
�ķ��̣�
��2�����^(gu��)�c(di��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c�p����(xi��n)
�c�p����(xi��n)![]() �Ѓɂ�(g��)��ͬ�Ľ��c(di��n)����(sh��)��(sh��)
�Ѓɂ�(g��)��ͬ�Ľ��c(di��n)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��3���O(sh��)��2����ֱ��(xi��n)![]() �c�p����(xi��n)
�c�p����(xi��n)![]() ����
����![]() �ɂ�(g��)��ͬ���c(di��n)�����Ծ�(xi��n)��
�ɂ�(g��)��ͬ���c(di��n)�����Ծ�(xi��n)��![]() ��ֱ���ĈA��(j��ng)�^(gu��)����(bi��o)ԭ�c(di��n)����(sh��)��(sh��)
��ֱ���ĈA��(j��ng)�^(gu��)����(bi��o)ԭ�c(di��n)����(sh��)��(sh��)![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���タ(xi��n)![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ��
��![]() ��
��![]() �S�ϵ��c(di��n).
�S�ϵ��c(di��n).
��1���^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c
�c![]() ���У����о�(xi��n)
���У����о�(xi��n)![]() �ķ��̣�
�ķ��̣�
��2����������^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c���タ(xi��n)����
�c���タ(xi��n)����![]() ��
��![]() ���c(di��n)����ֱ��(xi��n)
���c(di��n)����ֱ��(xi��n)![]() �c
�c![]() �ăAб�ǻ��a(b��)����(sh��)��(sh��)
�ăAб�ǻ��a(b��)����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���������F![]() �У�����
�У�����![]() ��߅�L(zh��ng)��2�������Σ�
��߅�L(zh��ng)��2�������Σ�![]() ����
����![]() �������F
�������F![]() ���w�e
���w�e![]() ��M��
��M��![]() �����c(di��n).
�����c(di��n).
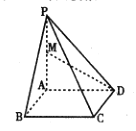
��1������ֱ��(xi��n)![]() �c
�c![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��2�����c(di��n)B��ƽ��![]() �ľ��x.
�ľ��x.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��) �ĈD��ǡ�ý�(j��ng)�^(gu��)����(g��)���ޣ��t��(sh��)��(sh��)
�ĈD��ǡ�ý�(j��ng)�^(gu��)����(g��)���ޣ��t��(sh��)��(sh��)![]() ��ȡֵ������______��
��ȡֵ������______��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)���x��![]() �ϵĺ���(sh��)
�ϵĺ���(sh��)![]() .
.
��1����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2��������![]() ��ʹ��
��ʹ��![]() ��������(sh��)��(sh��)
��������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��3�����x:�����(sh��)��(sh��)![]() �M(m��n)��
�M(m��n)��![]() �� ��ô�Q(ch��ng)
�� ��ô�Q(ch��ng)![]() ��
��![]() ���ӽ�
���ӽ�![]() .��(du��)�ڣ�2���е�
.��(du��)�ڣ�2���е�![]() ��
��![]() ����(w��n):
����(w��n):![]() ��
��![]() �Ă�(g��)���ӽ�
�Ă�(g��)���ӽ�![]() �����f(shu��)������.
�����f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �ăɂ�(g��)���c(di��n)�քe��
�ăɂ�(g��)���c(di��n)�քe��![]() ���L(zh��ng)�S�L(zh��ng)��
���L(zh��ng)�S�L(zh��ng)��![]() ��
��
��������E�A![]() �Ę�(bi��o)��(zh��n)���̼��x���ʣ�
�Ę�(bi��o)��(zh��n)���̼��x���ʣ�
�������^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)�����c(di��n)
���c(di��n)�����c(di��n)![]() �M(m��n)��
�M(m��n)��![]() �����C�����c(di��n)
�����C�����c(di��n)![]() ��(g��u)�ɵ�����(xi��n)
��(g��u)�ɵ�����(xi��n)![]() �P(gu��n)��ֱ��(xi��n)
�P(gu��n)��ֱ��(xi��n)![]() ��(du��)�Q(ch��ng)��
��(du��)�Q(ch��ng)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����x׃�Q![]() ��ƽ���(n��i)���c(di��n)
��ƽ���(n��i)���c(di��n)![]() ׃�Q��ƽ���(n��i)���c(di��n)
׃�Q��ƽ���(n��i)���c(di��n)![]() ��������(xi��n)
��������(xi��n)![]() ��(j��ng)׃�Q
��(j��ng)׃�Q![]() ��õ�����(xi��n)
��õ�����(xi��n)![]() ������(xi��n)
������(xi��n)![]() ��(j��ng)׃�Q
��(j��ng)׃�Q![]() ��õ�����(xi��n)
��õ�����(xi��n)![]() �����������(l��i)�ƣ�����(xi��n)
�����������(l��i)�ƣ�����(xi��n)![]() ��(j��ng)׃�Q
��(j��ng)׃�Q![]() ��õ�����(xi��n)
��õ�����(xi��n)![]() ����(d��ng)
����(d��ng)![]() �r(sh��)��ӛ����(xi��n)
�r(sh��)��ӛ����(xi��n)![]() �c
�c![]() ��
��![]() �S�����S�Ľ��c(di��n)��
�S�����S�Ľ��c(di��n)��![]() ��
��![]() ��ijͬ�W(xu��)�о����J(r��n)������(xi��n)
��ijͬ�W(xu��)�о����J(r��n)������(xi��n)![]() �����������|(zh��)���ٌ�(du��)�����
�����������|(zh��)���ٌ�(du��)�����![]() ������(xi��n)
������(xi��n)![]() ���P(gu��n)��ԭ�c(di��n)��(du��)�Q(ch��ng)���ڌ�(du��)�����
���P(gu��n)��ԭ�c(di��n)��(du��)�Q(ch��ng)���ڌ�(du��)�����![]() ������(xi��n)
������(xi��n)![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ���ی�(du��)�����
���ی�(du��)�����![]() ������(xi��n)
������(xi��n)![]() ���ھ���
���ھ���![]() ����߅�磩�ă�(n��i)��������
����߅�磩�ă�(n��i)��������![]() ������(bi��o)��
������(bi��o)��![]() ����ӛ����
����ӛ����![]() ����e��
����e��![]() ���t
���t![]() �������������_�Y(ji��)Փ����̖(h��o)��_______.
�������������_�Y(ji��)Փ����̖(h��o)��_______.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com