
【題目】為了推進分級診療,實現“基層首診、雙向轉診、急慢分治、上下聯動”的診療模式,某地區自2016年起全面推行家庭醫生簽約服務.已知該地區居民約為2000萬,從1歲到101歲的居民年齡結構的頻率分布直方圖如圖1所示.為了解各年齡段居民簽約家庭醫生的情況,現調查了1000名年滿18周歲的居民,各年齡段被訪者簽約率如圖2所示.
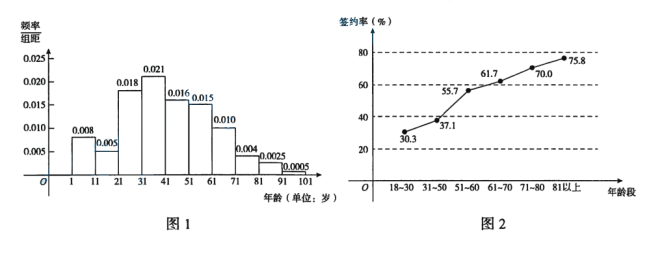
(1)估計該地區年齡在71~80歲且已簽約家庭醫生的居民人數;
(2)若以圖2中年齡在71~80歲居民簽約率作為此地區該年齡段每個居民簽約家庭醫生的概率,則從該地區年齡在71~80歲居民中隨機抽取兩人,求這兩人中恰有1人已簽約家庭醫生的概率;
(3)據統計,該地區被訪者的簽約率約為![]() .為把該地區年滿18周歲居民的簽約率提高到
.為把該地區年滿18周歲居民的簽約率提高到![]() 以上,應著重提高圖2中哪個年齡段的簽約率?并結合數據對你的結論作出解釋.
以上,應著重提高圖2中哪個年齡段的簽約率?并結合數據對你的結論作出解釋.
【答案】(1)56萬,(2)0.42,(3)應著重提高31-50這個年齡段的簽約率,見解析.
【解析】
(1)先由圖1算出年齡在71-80歲的居民人數,然后由圖2得到年齡在71-80歲的居民簽約率,即可算出答案;
(2)由圖2得到年齡段在71-80的每個居民簽約家庭醫生的概率,然后即可算出答案;
(3)根據圖1算出每個年齡段的人數,然后結合簽約率即可得到答案.
(1)由題知該地區居民約為2000萬,由圖1知,該地區年齡在71-80歲的居民人數為![]() 萬.
萬.
由圖2知,年齡在71-80歲的居民簽約率為0.7,所以該地區年齡在71-80歲且已簽約家庭醫生的居民人數為:![]() 萬.
萬.
(2)由題知此地區年齡段在71-80的每個居民簽約家庭醫生的概率為![]() ,且每個居民之間是否簽約都是獨立的,
,且每個居民之間是否簽約都是獨立的,
所以設“從該地區年齡在71-80歲居民中隨機抽取兩人”為事件![]() ,隨機變量為
,隨機變量為![]() ,
,
這兩人中恰有1人已簽約家庭醫生的概率為:![]()
(3)由圖1,2知:
年齡段 | 該地區人數(萬) | 簽約率 |
18-30 |
大于360,小于460 | 30.3 |
31-40,41-50 |
| 37.1 |
51-60 |
| 55.7 |
61-70 |
| 61.7 |
71-80 |
| 70 |
80以上 |
| 75.8 |
由以上數據可知這個地區在31-50這個年齡段的人為740萬,基數較其他年齡段是最大的,且簽約率為![]() ,非常低,
,非常低,
所以為把該地區滿18周歲居民的簽約率提高到![]() 以上,應著重提高31-50這個年齡段的簽約率.
以上,應著重提高31-50這個年齡段的簽約率.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案科目:高中數學 來源: 題型:
【題目】某學校高中三個年級共有4000人,為了了解各年級學周末在家的學習情況,現通過分層抽樣的方法獲得相關數據如下(單位:小時),其中高一學生周末的平均學習時間記為![]() .
.
高一:14 15 15.5 16.5 17 17 18 19
高二:15 16 16 16 17 17 18.5
高三:16 17 18 21.5 24
(1)求每個年級的學生人數;
(2)從高三被抽查的同學中隨機抽取2人,求2人學習時間均超過![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為實數,用
為實數,用![]() 表示不超過
表示不超過![]() 的最大整數,例如
的最大整數,例如![]() ,
,![]() ,
,![]() ,對于函數
,對于函數![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() ,則稱函數
,則稱函數![]() 是“
是“![]() 函數”.
函數”.
(1)判斷函數![]() ,
,![]() 是否是“
是否是“![]() 函數”;
函數”;
(2)設函數![]() 是定義在
是定義在![]() 上的周期函數,其最小正周期是
上的周期函數,其最小正周期是![]() ,若
,若![]() 不是“
不是“![]() 函數”,求
函數”,求![]() 的最小值;
的最小值;
(3)若函數![]() 是“
是“![]() 函數”,求
函數”,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了比較兩種治療失眠癥的藥(分別稱為![]() 藥,
藥,![]() 藥)的療效,某機構隨機地選取
藥)的療效,某機構隨機地選取![]() 位患者服用
位患者服用![]() 藥,
藥,![]() 位患者服用
位患者服用![]() 藥,觀察這
藥,觀察這![]() 位患者的睡眠改善情況.這些患者服用一段時間后,根據患者的日平均增加睡眠時間(單位:
位患者的睡眠改善情況.這些患者服用一段時間后,根據患者的日平均增加睡眠時間(單位:![]() ),以整數部分當莖,小數部分當葉,繪制了如下莖葉圖:
),以整數部分當莖,小數部分當葉,繪制了如下莖葉圖:
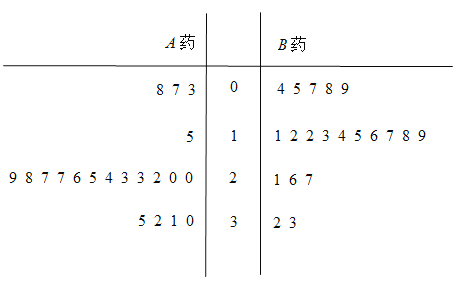
(1)根據莖葉圖判斷哪種藥對增加睡眠時間更有效?并說明理由;
(2)求這![]() 名患者日平均增加睡眠時間的中位數
名患者日平均增加睡眠時間的中位數![]() ,并將日平均增加睡眠時間超過
,并將日平均增加睡眠時間超過![]() 和不超過
和不超過![]() 的患者人數填入下面的列聯表:
的患者人數填入下面的列聯表:
超過 | 不超過 | |
服用 | ||
服用 |
(3)根據(2)中的列聯表,能否有![]() 的把握認為
的把握認為![]() 兩種藥的療效有差異?
兩種藥的療效有差異?
附: 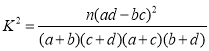 .
.
| 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com