
【題目】已知函數![]() (
(![]() )的單調遞減區間為
)的單調遞減區間為 .
.
(I)求a的值;
(II)證明:當![]() 時,
時,![]() ;
;
(III)若存在![]() ,使得當
,使得當![]() 時,恒有
時,恒有![]() ,求實數k的取值范圍.
,求實數k的取值范圍.
【答案】(I)![]() ;(II)證明見解析;(III)
;(II)證明見解析;(III)![]() .
.
【解析】
(I)由題意知![]() 為方程
為方程![]() 的一個根,求出
的一個根,求出![]() 后注意檢驗一下.
后注意檢驗一下.
(II)構造![]() ,通過研究其單調性,證明
,通過研究其單調性,證明![]() 即可.
即可.
(III)根據(II),分![]() 、
、![]() 、
、![]() 三種情況討論,前兩種情況容易證明不存在滿足條件的
三種情況討論,前兩種情況容易證明不存在滿足條件的![]() 值,當
值,當![]() 時,令
時,令![]() ,通過研究
,通過研究![]() 的導數,進一步研究其單調性,找到
的導數,進一步研究其單調性,找到![]() 值并證明
值并證明![]() 即可.
即可.
解:(I)![]() 的定義域為
的定義域為![]() .
.
![]() .
.
由題意知![]() 為方程
為方程![]() 的一個根.
的一個根.
所以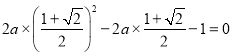 ,解得
,解得![]() .
.
當![]() 時,
時,![]() ,得
,得![]()
![]() 的單調遞減區間為
的單調遞減區間為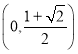 ,符合題意.
,符合題意.
(II)設![]() ,
,
則![]() .
.
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞增.
上單調遞增.
所以當![]() 時,
時,![]() ,即
,即![]() .
.
(III)當![]() 時,由(II)知不存在符合條件的m.
時,由(II)知不存在符合條件的m.
當![]() 時,對于
時,對于![]() ,
,![]() ,故不存在符合條件的m.
,故不存在符合條件的m.
當![]() 時,令
時,令![]() ,
,
則![]() .
.
令![]() ,得
,得![]() ,
,![]() .
.
因為當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞減,
上單調遞減,![]() ,
,
即![]() ,此時取
,此時取![]() 即可.
即可.
綜上所述,k的取值范圍是![]() .
.


 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案科目:高中數學 來源: 題型:
【題目】拋物線![]() 的焦點為F,P為其上一動點,設直線l與拋物線C相交于A,B兩點,點
的焦點為F,P為其上一動點,設直線l與拋物線C相交于A,B兩點,點![]() 下列結論正確的是( )
下列結論正確的是( )
A.|PM| +|PF|的最小值為3
B.拋物線C上的動點到點![]() 的距離最小值為3
的距離最小值為3
C.存在直線l,使得A,B兩點關于![]() 對稱
對稱
D.若過A、B的拋物線的兩條切線交準線于點T,則A、B兩點的縱坐標之和最小值為2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了推進分級診療,實現“基層首診、雙向轉診、急慢分治、上下聯動”的診療模式,某地區自2016年起全面推行家庭醫生簽約服務.已知該地區居民約為2000萬,從1歲到101歲的居民年齡結構的頻率分布直方圖如圖1所示.為了解各年齡段居民簽約家庭醫生的情況,現調查了1000名年滿18周歲的居民,各年齡段被訪者簽約率如圖2所示.
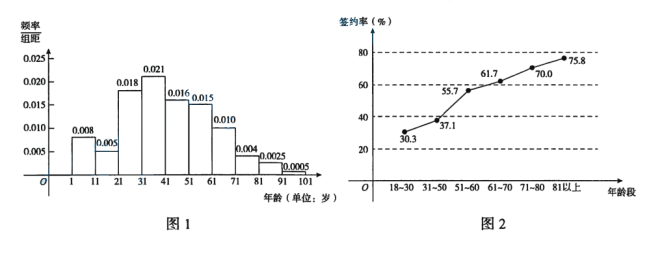
(1)估計該地區年齡在71~80歲且已簽約家庭醫生的居民人數;
(2)若以圖2中年齡在71~80歲居民簽約率作為此地區該年齡段每個居民簽約家庭醫生的概率,則從該地區年齡在71~80歲居民中隨機抽取兩人,求這兩人中恰有1人已簽約家庭醫生的概率;
(3)據統計,該地區被訪者的簽約率約為![]() .為把該地區年滿18周歲居民的簽約率提高到
.為把該地區年滿18周歲居民的簽約率提高到![]() 以上,應著重提高圖2中哪個年齡段的簽約率?并結合數據對你的結論作出解釋.
以上,應著重提高圖2中哪個年齡段的簽約率?并結合數據對你的結論作出解釋.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】非典和新冠肺炎兩場疫情告訴我們:應堅決杜絕食用野生動物,提倡文明健康,綠色環保的生活方式.在我國抗擊新冠肺炎期間,某校開展一次有關病毒的網絡科普講座.高三年級男生60人,女生40人參加.按分層抽樣的方法,在100名同學中選出5人,則男生中選出________人.再從此5人中選出兩名同學作為聯絡人,則這兩名聯絡人中男女都有的概率是________.(第1空2分,第2空3分)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 交橢圓
交橢圓![]() 于兩點
于兩點![]() ,
,![]() .
.
(1)若![]() ,且點
,且點![]() 滿足
滿足![]() ,證明:點
,證明:點![]() 不在橢圓
不在橢圓![]() 上;
上;
(2)若橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,直線
,直線![]() 與線段
與線段![]() 和橢圓
和橢圓![]() 的短軸分別交于兩個不同點
的短軸分別交于兩個不同點![]() ,
,![]() ,且
,且![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)函數![]() ,討論
,討論![]() 的單調性;
的單調性;
(2)曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,是否存在這樣的點
,是否存在這樣的點![]() 使得直線
使得直線![]() 與曲線
與曲線![]() 也相切,若存在,判斷滿足條件的點
也相切,若存在,判斷滿足條件的點![]() 的個數,若不存在,請說明理由.
的個數,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】.對于n∈N*(n≥2),定義一個如下數陣: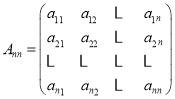 ,其中對任意的1≤i≤n,1≤j≤n,當i能整除j時,aij=1;當i不能整除j時,aij=0.設
,其中對任意的1≤i≤n,1≤j≤n,當i能整除j時,aij=1;當i不能整除j時,aij=0.設![]() .
.
(Ⅰ)當n=6時,試寫出數陣A66并計算![]() ;
;
(Ⅱ)若[x]表示不超過x的最大整數,求證:![]() ;
;
(Ⅲ)若![]() ,
,![]() ,求證:g(n)﹣1<f(n)<g(n)+1.
,求證:g(n)﹣1<f(n)<g(n)+1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花圃為提高某品種花苗質量,開展技術創新活動,在![]() 實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各50株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖,記綜合評分為80分及以上的花苗為優質花苗.
實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各50株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖,記綜合評分為80分及以上的花苗為優質花苗.
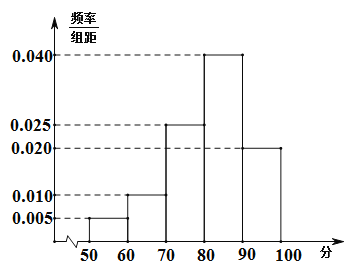
(1)用樣本估計總體,以頻率作為概率,若在![]() 兩塊實驗地隨機抽取3株花苗,求所抽取的花苗中優質花苗數的分布列和數學期望;
兩塊實驗地隨機抽取3株花苗,求所抽取的花苗中優質花苗數的分布列和數學期望;
(2)填寫下面的列聯表,并判斷是否有99%的把握認為優質花苗與培育方法有關.
優質花苗 | 非優質花苗 | 合計 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合計 |
附:下面的臨界值表僅供參考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(參考公式: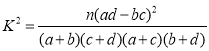 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘著名數學家阿波羅尼斯與歐幾里得、阿基米德齊名.他發現:“平面內到兩個定點![]() 的距離之比為定值
的距離之比為定值![]() 的點的軌跡是圓”.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓在平面直角坐標系
的點的軌跡是圓”.后來,人們將這個圓以他的名字命名,稱為阿波羅尼斯圓,簡稱阿氏圓在平面直角坐標系![]() 中,
中,![]() 點
點![]() .設點
.設點![]() 的軌跡為
的軌跡為![]() ,下列結論正確的是( )
,下列結論正確的是( )
A. ![]() 的方程為
的方程為![]()
B. 在![]() 軸上存在異于
軸上存在異于![]() 的兩定點
的兩定點![]() ,使得
,使得![]()
C. 當![]() 三點不共線時,射線
三點不共線時,射線![]() 是
是![]() 的平分線
的平分線
D. 在![]() 上存在點
上存在點![]() ,使得
,使得![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com