
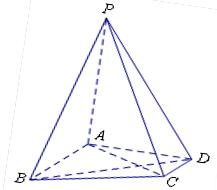
在四棱錐 中,
中,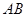 //
//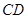 ,
,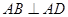 ,
,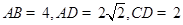 ,
,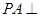 平面
平面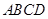 ,
,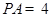 .
. 
(1)求證: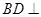 平面
平面 ;
;
(2)求異面直線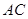 與
與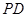 所成角的余弦值;
所成角的余弦值;
(3)設(shè)點(diǎn)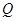 為線段
為線段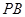 上一點(diǎn),且直線
上一點(diǎn),且直線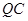 與平面
與平面 所成角的正弦值為
所成角的正弦值為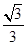 ,求
,求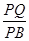 的值.
的值.
(1)見(jiàn)解析(2)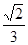 ,(3)
,(3)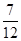
解析試題分析:(1)建立如圖所示坐標(biāo)系,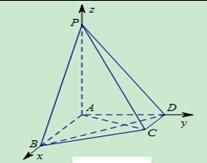
寫(xiě)出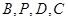 坐標(biāo),可得
坐標(biāo),可得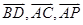 坐標(biāo),由
坐標(biāo),由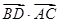 =
= ,
, =
= 知
知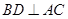 ,
,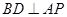 .所以
.所以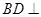 平面
平面 ;(2)由
;(2)由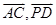 向量的夾角可知異成直線
向量的夾角可知異成直線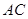 與
與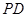 所成角;(3)
所成角;(3)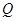 為線段
為線段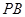 上一點(diǎn),設(shè)
上一點(diǎn),設(shè) 其中
其中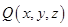 可得
可得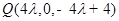 ,由直線
,由直線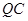 與平面
與平面 所成角的正弦值為
所成角的正弦值為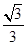 ,利用
,利用 與平面
與平面 的法向量
的法向量 夾角,可得
夾角,可得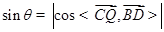 .其中
.其中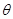 為直線
為直線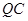 與平面
與平面 所成角.
所成角.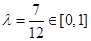 .即
.即 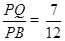 .
.
試題解析:(1)證明: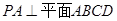 因?yàn)椋?img src="http://thumb.zyjl.cn/pic5/tikupic/ee/a/tiiot.png" style="vertical-align:middle;" />,所以以
因?yàn)椋?img src="http://thumb.zyjl.cn/pic5/tikupic/ee/a/tiiot.png" style="vertical-align:middle;" />,所以以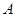 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),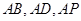 所在的直線分別為
所在的直線分別為 軸、
軸、 軸、
軸、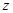 軸建立空間直角坐標(biāo)系, 1分
軸建立空間直角坐標(biāo)系, 1分
則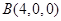 ,
,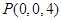 ,
,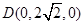 ,
,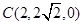 .
.
所以  ,
,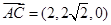 ,
,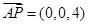 , 2分
, 2分
所以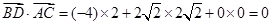 ,
,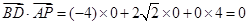 .
.
所以 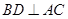 ,
,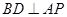 .
.
因?yàn)?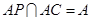 ,
,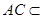 平面
平面 ,
,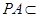 平面
平面 ,
,
所以 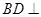 平面
平面 . 4分
. 4分
(2) 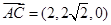 ,
,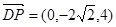 5分
5分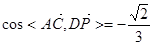
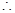 異成直線
異成直線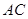 與
與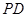 所成角的余弦值
所成角的余弦值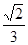 8分
8分
(3)解:設(shè) (其中
(其中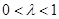 ),
),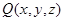 ,直線
,直線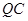 與平面
與平面 所成角為
所成角為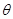 .
.
所以 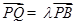 .所以
.所以 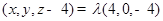 .
.


 53隨堂測(cè)系列答案
53隨堂測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
在如圖所示的多面體中,底面BCFE是梯形,EF//BC,又EF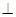 平面AEB,AE
平面AEB,AE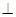 EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G為BC的中點(diǎn).
EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G為BC的中點(diǎn).
(1)求證:AB//平面DEG;
(2)求證:BD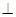 EG;
EG;
(3)求二面角C—DF—E的正弦值.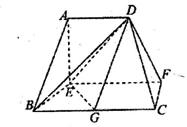
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,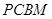 是直角梯形,∠
是直角梯形,∠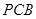 =90°,
=90°,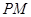 ∥
∥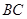 ,
,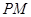 =1,
=1,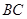 =2,又
=2,又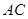 =1,∠
=1,∠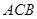 =120°,
=120°,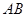 ⊥
⊥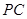 ,直線
,直線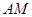 與直線
與直線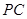 所成的角為60°.
所成的角為60°.
(1)求二面角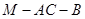 的的余弦值;
的的余弦值;
(2)求點(diǎn) 到面
到面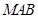 的距離.
的距離.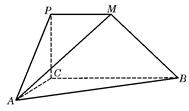
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,幾何體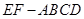 中,
中,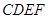 為邊長(zhǎng)為
為邊長(zhǎng)為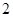 的正方形,
的正方形,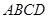 為直角梯形,
為直角梯形, ,
,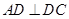 ,
,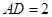 ,
, ,
,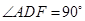 .
.
(1)求異面直線 和
和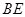 所成角的大小;
所成角的大小;
(2)求幾何體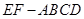 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,在四棱錐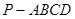 中,底面
中,底面 是正方形,側(cè)棱
是正方形,側(cè)棱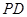 ⊥底面
⊥底面 ,
,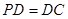 ,
,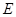 是
是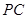 的中點(diǎn),作
的中點(diǎn),作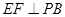 交
交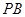 于點(diǎn)
于點(diǎn)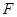 .
.
(1)證明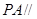 平面
平面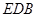 ;
;
(2)證明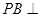 平面
平面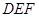 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖1,在△ABC中,BC=3,AC=6,∠C=90°,且DE∥BC,將△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如圖2。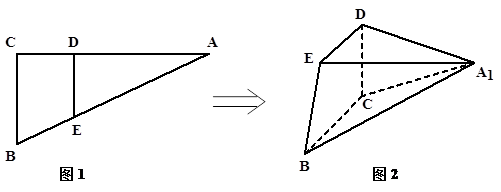
(1)求證:BC⊥平面A1DC;
(2)若CD=2,求BE與平面A1BC所成角的正弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知平行四邊形ABCD中,AB=6,AD=10,BD=8,E是線段AD的中點(diǎn).沿直線BD將△BCD翻折成△BC D,使得平面BC
D,使得平面BC D
D 平面ABD.
平面ABD.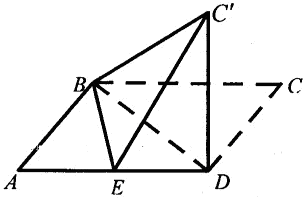
(1)求證:C'D 平面ABD;
平面ABD;
(2)求直線BD與平面BEC'所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
)如圖所示,在三棱錐P-ABC中,AB=BC=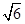 ,平面PAC⊥平面ABC,PD⊥AC于點(diǎn)D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于點(diǎn)D,AD=1,CD=3,PD= .
.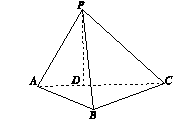
(1)證明:△PBC為直角三角形;
(2)求直線AP與平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖所示,四棱錐PABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD= ,F(xiàn)為PC的中點(diǎn),AF⊥PB.
,F(xiàn)為PC的中點(diǎn),AF⊥PB.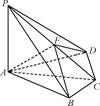
(1)求PA的長(zhǎng);
(2)求二面角B-AF-D的正弦值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com