已知函數f(x)=ex-ax-2.
(1)求f(x)的單調區間;
(2)若a=1,m為整數,且x>0時,不等式(m+1-x)f(x)+m-2-2x<0恒成立,求m的最大值.(可能用到的參數考數據:e=2.718,e2=7.389,e3=20.086)
【答案】
分析:(1)對f(x)進行求導,令f′(x)=0,求出極值點,利用導數研究函數的單調性;
(2)把a=1代入f(x),因為不等式(m+1-x)f(x)+m-2-2x<0,可得(m+1-x)(e
x-1)+m-2-2x<0,再利用分離變量法進行求解;
解答:解:(1)函數f(x)=e
x-ax-2,
f′(x)=e
x-a,若a≤0,則f′(x)>0,
f(x)在(-∞,+∞)上單調遞增,
若a>0,則x∈(-∞,lna)時,f′(x)>0;
當x∈(lna,+∞)上單調遞減,在(-∞,lna)上單調遞增,
(2)a=1,m為整數,且x>0時,不等式(m+1-x)f(x)+m-2-2x<0恒成立,
可得(m+1-x)(e
x-1)+m-2-2x<0,分離變量得,m<x-1+

令g(x)=x-1+
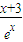
,x∈(0,+∞),
g′(x)=
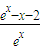
,
令g(x)=x-1+
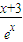
,x∈(0,+∞),g′(x)=
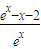
,
令h(x)=e
x-x-2,x∈(0,+∞),
由(1)可知h(x)在(0,+∞)上單調遞減,
又h(1)=e-3<0,h(

)=e
2-

>0,
∴必存在x
∈(1,

),使h(x
)=0,
當x∈(0,x
)時,g′(x)<0,g(x)單調遞減,
當x∈(x
,+∞)時,g′(x)>0,g(x)為單調遞減,
∴g(x)
min=g(x
)=x
-1+

,
∵x
是方程e
x-x-2=0的根,
∴e
x=x
+2,
∴g(x)
min=x
-1+
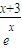
=x
-1+

=
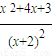
,
令m(x
)=
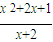
,x
∈(1,

),m′(x
)=
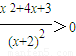
∴m(x
)在(1,

)上單調遞減,
∴m(x
)∈(

,
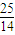
),即g(x)
max∈(

,
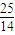
),
∴m的最大值為1.
點評:此題主要考查利用導數研究函數的單調性及其應用,解題的過程中用到常數分離法進行求解,是一道中檔題;


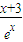 ,x∈(0,+∞),
,x∈(0,+∞),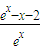 ,
,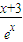 ,x∈(0,+∞),g′(x)=
,x∈(0,+∞),g′(x)=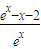 ,
, )=e2-
)=e2- >0,
>0, ),使h(x)=0,
),使h(x)=0, ,
,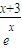 =x-1+
=x-1+ =
=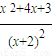 ,
,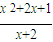 ,x∈(1,
,x∈(1, ),m′(x)=
),m′(x)=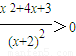
 )上單調遞減,
)上單調遞減, ,
,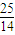 ),即g(x)max∈(
),即g(x)max∈( ,
,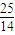 ),
),
