（幾何證明選講）（本小題滿分10分）如圖，MN為兩圓的公共弦，一條直線與兩圓及公共弦依次交于A，B，C，D，E，求證：AB·CD = BC·DE．
詳見解析
【解析】
試題分析：根據題意結合圓的性質，由相交弦定理，得AC·CD = MC·NC，和BC·CE = MC·NC．化簡即可得：AC·CD = BC·CE，對其整理即可（AB BC）·CD = BC·（CD DE），也即AB·CD BC·CD = BC·CD BC·DE，問題得證.
試題解析：證明：由相交弦定理，得
AC·CD = MC·NC．
BC·CE = MC·NC．
∴AC·CD = BC·CE．
即（AB BC）·CD = BC·（CD DE）．
也即AB·CD BC·CD = BC·CD BC·DE．
∴AB·CD = BC·DE．
考點：圓的相交弦定理
閱讀快車系列答案科目：高中數學 來源：2015屆江蘇省蘇州市高三上學期期中測試數學試卷（解析版） 題型：解答題
（本小題滿分10分）某校要進行特色學校評估驗收，有甲、乙、丙、丁、戊五位評估員將隨機去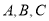
三個不同的班級進行隨班聽課，要求每個班級至少有一位評估員．
（1）求甲、乙同時去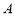
班聽課的概率；
（2）設隨機變量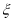
為這五名評估員去
班聽課的人數，求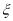
的分布列和數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
，則
的值為（ ）
B．
C．
D．
，則p＝ ．
在區間
上是單調減函數，則實數
的取值范圍是 ． 
的面積為
，且
．
的值；
，
，求△ABC的面積
．
與
在點
處的切線互相垂直，則
．
的解集是區間
的子集，則實數
的范圍為__________．
，則該圓的圓心到直線
的距離是 .