C
分析:先根據已知條件把f(2a+1)>f(-a+1)-f(3a)-3f(1)轉化為f[(2a+1)3a]>f(-a+1);進而得到f(|3a(2a+1)|)>f(|-a+1|)再結合其單調性推出|3a(2a+1)|<|-a+1|,平方解不等式即可求出答案.
解答:由f(xy)=f(x)+f(y)?f(1×1)=f(1)+f(1)?f(1)=0;
∴f(2a+1)>f(-a+1)-f(3a)-3f(1)
?f(2a+1)+f(3a)>f(-a+1)
?f[(2a+1)3a]>f(-a+1);①
∵f(x)定義在R且x不為零的偶函數;
∴①轉化為f(|3a(2a+1)|)>f(|-a+1|)②
∵函數在區間(-∞,0)上遞增,
∴函數在區間(0,+∞)上遞增,
∴②轉化為|3a(2a+1)|<|-a+1|?[3a(2a+1)]
2<(-a+1)
2?[3a(2a+1)-(-a+1)][3a(2a+1)+(-a+1)]<0?(6a
2+2a+1)(6a
2+4a-1)<0;
∵6a
2+2a+1=6(a+

)
2+

>0恒成立;
而6a
2+4a-1=6(a-

)(a+

)<0?

<a<

;
∵定義域內不含0,
∴2a+1≠0且1-a≠0且3a≠0;
故a≠-

且a≠0且a≠1.
∴滿足條件的a的取值范圍是:

<a<

且a≠0且a≠-

.
故選:C.
點評:本題主要考查函數奇偶性的應用以及抽象函數的應用.解決本題的關鍵在于把f(2a+1)>f(-a+1)-f(3a)-3f(1)轉化為f[(2a+1)3a]>f(-a+1).

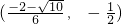
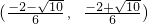
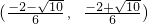 且a
且a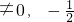
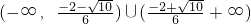
 )2+
)2+ >0恒成立;
>0恒成立; )(a+
)(a+ )<0?
)<0? <a<
<a< ;
; 且a≠0且a≠1.
且a≠0且a≠1. <a<
<a< 且a≠0且a≠-
且a≠0且a≠- .
.

 新思維寒假作業系列答案
新思維寒假作業系列答案

 且a
且a
