
 培優(yōu)好卷單元加期末卷系列答案
培優(yōu)好卷單元加期末卷系列答案 一線名師權威作業(yè)本系列答案
一線名師權威作業(yè)本系列答案科目:高中數學 來源:2010-2011學年遼寧省遼南協(xié)作體高一下學期期中考試數學(文) 題型:解答題
已知向量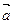 =(1,2),
=(1,2),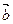 =(cosa,sina),設
=(cosa,sina),設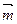 =
=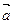 +t
+t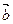 (
(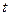 為實數).
為實數).
(1)若a=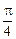 ,求當|
,求當|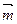 |取最小值時實數
|取最小值時實數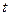 的值;
的值;
(2)若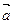 ⊥
⊥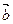 ,問:是否存在實數
,問:是否存在實數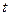 ,使得向量
,使得向量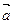 –
–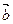 和向量
和向量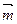 的夾角為
的夾角為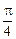 ,若存在,請求出t的值;若不存在,請說明理由.
,若存在,請求出t的值;若不存在,請說明理由.
(3)若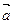 ⊥
⊥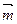 ,求實數
,求實數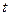 的取值范圍A,并判斷當
的取值范圍A,并判斷當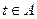 時函數
時函數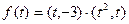 的單調性.
的單調性.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年遼寧省遼南協(xié)作體高一下學期期中考試數學(理) 題型:解答題
已知向量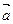 =(1,2),
=(1,2),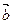 =(cosa,sina),設
=(cosa,sina),設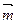 =
=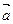 +t
+t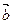 (
(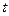 為實數).
為實數).
(1)若a=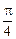 ,求當|
,求當|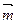 |取最小值時實數
|取最小值時實數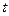 的值;
的值;
(2)若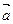 ⊥
⊥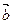 ,問:是否存在實數
,問:是否存在實數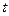 ,使得向量
,使得向量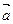 –
–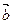 和向量
和向量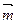 的夾角為
的夾角為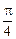 ,若存在,請求出t的值;若不存在,請說明理由.
,若存在,請求出t的值;若不存在,請說明理由.
(3)若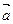 ⊥
⊥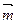 ,求實數
,求實數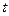 的取值范圍A,并判斷當
的取值范圍A,并判斷當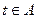 時函數
時函數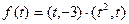 的單調性.
的單調性.
查看答案和解析>>
科目:高中數學 來源:2013屆遼寧省遼南協(xié)作體高一下學期期中考試數學(理) 題型:解答題
已知向量 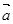 =(1,2) ,
=(1,2) ,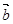 =(cosa,sina),設
=(cosa,sina),設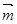 =
=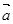 +t
+t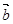 (
(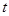 為實數).
為實數).
(1)若a=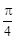 ,求當|
,求當|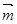 |取最小值時實數
|取最小值時實數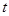 的值;
的值;
(2)若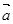 ⊥
⊥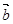 ,問:是否存在實數
,問:是否存在實數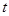 ,使得向量
,使得向量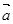 –
–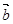 和向量
和向量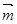 的夾角為
的夾角為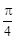 ,若存在,請求出t的值;若不存在,請說明理由.
,若存在,請求出t的值;若不存在,請說明理由.
(3)若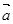 ⊥
⊥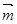 ,求實數
,求實數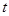 的取值范圍A,并判斷當
的取值范圍A,并判斷當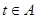 時函數
時函數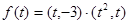 的單調性.
的單調性.
查看答案和解析>>
科目:高中數學 來源:2013屆遼寧省遼南協(xié)作體高一下學期期中考試數學(文) 題型:解答題
已知向量 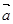 =(1,2) ,
=(1,2) ,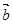 =(cosa,sina),設
=(cosa,sina),設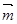 =
=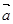 +t
+t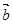 (
(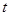 為實數).
為實數).
(1)若a=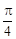 ,求當|
,求當|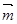 |取最小值時實數
|取最小值時實數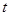 的值;
的值;
(2)若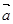 ⊥
⊥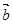 ,問:是否存在實數
,問:是否存在實數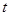 ,使得向量
,使得向量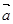 –
–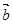 和向量
和向量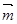 的夾角為
的夾角為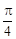 ,若存在,請求出t的值;若不存在,請說明理由.
,若存在,請求出t的值;若不存在,請說明理由.
(3)若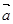 ⊥
⊥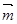 ,求實數
,求實數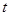 的取值范圍A,并判斷當
的取值范圍A,并判斷當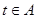 時函數
時函數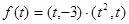 的單調性.
的單調性.
查看答案和解析>>
科目:高中數學 來源:2013屆山東省高一下學期期末考試數學 題型:解答題
已知向量 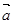 =(1,2) ,
=(1,2) ,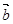 =(cosa,sina),設
=(cosa,sina),設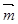 =
=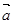 +t
+t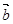 (
(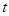 為實數).
為實數).
(1)若a=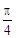 ,求當|
,求當|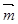 |取最小值時實數
|取最小值時實數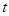 的值;
的值;
(2)若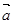 ⊥
⊥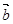 ,問:是否存在實數
,問:是否存在實數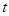 ,使得向量
,使得向量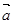 –
–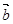 和向量
和向量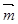 的夾角為
的夾角為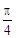 ,若存在,請求出t的值;若不存在,請說明理由.
,若存在,請求出t的值;若不存在,請說明理由.
(3)若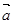 ⊥
⊥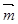 ,求實數
,求實數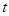 的取值范圍A,并判斷當
的取值范圍A,并判斷當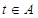 時函數
時函數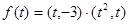 的單調性.
的單調性.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com