
���}Ŀ����֪![]() ������(sh��)
������(sh��)![]() .
.
��1��ӑՓ![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����(du��)![]() ������ʽ
������ʽ![]() ���������
���������![]() ��ȡֵ������
��ȡֵ������
��3����֪��(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() �Ѓɂ�(g��)���c(di��n)
�Ѓɂ�(g��)���c(di��n)![]() ��
��![]() �����C��
�����C��![]() .
.
���𰸡�(1)Ҋ����(2) ![]() ��3��Ҋ����
��3��Ҋ����
��������
ԇ�}��������1�����![]() ���փɷN��rӑՓ
���փɷN��rӑՓ![]() �ķ������ڶ��x���(n��i)���քe��
�ķ������ڶ��x���(n��i)���քe��![]() ���
���![]() �ķ������ɵú���(sh��)
�ķ������ɵú���(sh��)![]() ���^(q��)�g��
���^(q��)�g��![]() ���
���![]() �ķ������ɵú���(sh��)
�ķ������ɵú���(sh��)![]() �Ĝp�^(q��)�g����2���փɷN��rӑՓ����(d��ng)
�Ĝp�^(q��)�g����2���փɷN��rӑՓ����(d��ng)![]() ������һ�κ���(sh��)�����|(zh��)��⣬��(d��ng)
������һ�κ���(sh��)�����|(zh��)��⣬��(d��ng)![]() �r(sh��)��
�r(sh��)��![]()
![]() ���O(sh��)
���O(sh��)![]() ��ֻ����
��ֻ����![]() ���ɣ���3����
���ɣ���3����![]() ��ԭ����ʽ�D(zhu��n)�����C��
��ԭ����ʽ�D(zhu��n)�����C��![]() ����
����![]() ����
����![]() ������
������![]() �ăɂ�(g��)���c(di��n)
�ăɂ�(g��)���c(di��n)![]() �����Ì�(d��o)��(sh��)�о�����(sh��)�Ć��{(di��o)�ԣ�ֻ���C��ֻ���C
�����Ì�(d��o)��(sh��)�о�����(sh��)�Ć��{(di��o)�ԣ�ֻ���C��ֻ���C![]()
![]() ���ɵýY(ji��)Փ.
���ɵýY(ji��)Փ.
ԇ�}����������1��![]() ����
����![]() ��
��
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
��(d��ng)![]() �r(sh��)�����]
�r(sh��)�����]![]() �r(sh��)����
�r(sh��)����![]()
![]() ��
��
��![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ���{(di��o)�f����
���{(di��o)�f����
��![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ���{(di��o)�f��.
���{(di��o)�f��.
��2������һ������׃���x��
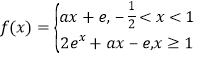 ��
��
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��
��
![]() .
.
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]()
![]() ��
��
�O(sh��)![]() ����
����![]()
![]() ��
��
��![]() ��
��![]() ���{(di��o)�f�p��
���{(di��o)�f�p��
��![]() ����
����![]() ��
��
�C��������![]() .
.
������������ֵ����
��![]() ��ֻ��
��ֻ��![]() ��
��![]() ��
��
�ɣ�1���ɵã�
�ٮ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
��![]() ���ɣ���ã�
���ɣ���ã�![]() ��
��
��![]() .
.
�ڮ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ���{(di��o)�f����
���{(di��o)�f����
��![]() ��
��
��![]() ��
��
��![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ���{(di��o)�f����
���{(di��o)�f����
��![]() ��
��
��![]() ����
����![]() ��
��
�O(sh��)![]() ���t
���t![]() ��
��
��![]() ��
��![]() ���{(di��o)�f�p��
���{(di��o)�f�p��
��![]() ������ԭ����ʽ�o(w��)��.
������ԭ����ʽ�o(w��)��.
����̎Ҳ����(g��u)�캯��(sh��)��![]() ���@Ȼ
���@Ȼ![]() �r(sh��)����ʽС���㣬�����C����
�r(sh��)����ʽС���㣬�����C����
�C��������![]() .
.
��3��ע�![]() ���������C������ʽ�D(zhu��n)�����C��
���������C������ʽ�D(zhu��n)�����C��![]() ��
��
��![]() ����
����![]() ��
��
����![]() �ăɂ�(g��)���c(di��n)
�ăɂ�(g��)���c(di��n)![]() .
.
����һ��
��![]() �ɵã�
�ɵã�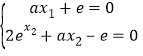 ��
��
�� ����
����![]() ��
��
��![]() ���t
���t![]() ��
��
��![]() ��
��![]() ���t��(d��ng)
���t��(d��ng)![]() �r(sh��)��
�r(sh��)��
![]() ��
��
��![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ����
����![]() ��
��
��![]() ��
��![]() ���{(di��o)�f�p��
���{(di��o)�f�p��![]() ����
����![]() ��
��
��![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() �����{(di��o)�f�p��
�����{(di��o)�f�p��
��![]() .
.
��������ͬ����һ��֪![]() �����濼�]�C��
�����濼�]�C��![]() ��
��
��![]() ��
��
���C��![]() ����
����![]() ��
��
����ֻ���C![]() ����
����![]() ��
��
����ֻ���C![]()
![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ���{(di��o)�f�p��
���{(di��o)�f�p��
��![]() ��
��
��![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ��
��
��![]()
![]() ��
��
����![]() ���C��
���C��
��![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() �����{(di��o)�f�p��
�����{(di��o)�f�p��
��![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���κ���(sh��)![]() �M��
�M��![]() ����
����![]() ��
��
![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() �O(sh��)
�O(sh��)![]() �������ڌ�(sh��)��(sh��)a��bʹ��
�������ڌ�(sh��)��(sh��)a��bʹ��![]() ����a��ȡֵ������
����a��ȡֵ������
![]() ��(du��)����
��(du��)����![]() ��
��![]() ����
����![]() ���������(sh��)��(sh��)t��ȡֵ������
���������(sh��)��(sh��)t��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ�У��c(di��n)![]() ��
��![]() �քe���p����
�քe���p����![]() �����ҽ��c(di��n)���p����
�����ҽ��c(di��n)���p����![]() ���x���ʞ�
���x���ʞ�![]() ���c(di��n)
���c(di��n)![]() ���p����
���p����![]() �ϣ�����
�ϣ�����![]() �S�ϵĄ�(d��ng)�c(di��n)
�S�ϵĄ�(d��ng)�c(di��n)![]() �c��(d��ng)�c(di��n)
�c��(d��ng)�c(di��n)![]() �P(gu��n)��ԭ�c(di��n)
�P(gu��n)��ԭ�c(di��n)![]() ��(du��)�Q������߅��
��(du��)�Q������߅��![]() �����L(zh��ng)��
�����L(zh��ng)��![]() .
.
(1)���(d��ng)�c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
(2)�^(gu��)�c(di��n)![]() ��ֱ����
��ֱ����![]() ��܉�E
��܉�E![]() ��
��![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() ��
��![]() ��һ�c(di��n)���ҝM��
��һ�c(di��n)���ҝM��![]() ������
������![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(ji��)�^(gu��)�ס��ҡ�������Մ?w��)������P(gu��n)![]() ���Ӱ
���Ӱ![]() ��
��![]() ��
��![]() ����r.
����r.
���f(shu��)���қ](m��i)�п��^(gu��)�Ӱ![]() ��������
��������![]() ���Ӱ�҂�?n��i)���(g��)�����^(gu��)��
���Ӱ�҂�?n��i)���(g��)�����^(gu��)��
���f(shu��)�������Ӱ����![]() ���Ӱ�҂�?n��i)�����ֻ��һ�˿��^(gu��)��
���Ӱ�҂�?n��i)�����ֻ��һ�˿��^(gu��)��
���f(shu��)���Һͼ����Ӱ��![]() ����ͬ����
����ͬ����![]() ����ͬ.
����ͬ.
�����������f(shu��)������Ԓ���t�ɴ˿��Д������Ӱ���ҿ��^(gu��)�IJ���(sh��)�ǣ� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������FE-ABCD�У�AE��DE��CD��ƽ��ADE��AB��ƽ��ADE��CD=DA=6��AB=2��DE=3.
��I�������FC-ADE���w�e��
��II�����C��ƽ��ACE��ƽ��CDE��
��III���ھ���DE���Ƿ����һ�c(di��n)F��ʹAF��ƽ��BCE�������ڣ����![]() ��ֵ���������ڣ��f(shu��)������.
��ֵ���������ڣ��f(shu��)������.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������ε�����(g��)��c(di��n)������(bi��o)�քe��![]() ��
��![]() ��
��![]() ���tԓ�����ε����ģ���߅�о����c(di��n)��������(bi��o)��
���tԓ�����ε����ģ���߅�о����c(di��n)��������(bi��o)��![]() .��@��(g��)�Y(ji��)Փ���B�������w��һ��(g��)��c(di��n)���䌦(du��)�����������ĵľ��ηQ�������w���о��������w���ėl�о�����һ�c(di��n)��ԓ�c(di��n)�Q�������w������.�������w���Ă�(g��)��c(di��n)�Ŀ��g����(bi��o)�քe��
.��@��(g��)�Y(ji��)Փ���B�������w��һ��(g��)��c(di��n)���䌦(du��)�����������ĵľ��ηQ�������w���о��������w���ėl�о�����һ�c(di��n)��ԓ�c(di��n)�Q�������w������.�������w���Ă�(g��)��c(di��n)�Ŀ��g����(bi��o)�քe��![]() ��
��![]() ��
��![]() ��
��![]() ���tԓ�����w�����ĵ�����(bi��o)�飨 ��
���tԓ�����w�����ĵ�����(bi��o)�飨 ��
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����![]() ����
����![]() �ăɂ�(g��)��(n��i)��.��������(g��)�l���У���
�ăɂ�(g��)��(n��i)��.��������(g��)�l���У���![]() ���ij�ֱ�Ҫ�l���Ă�(g��)��(sh��)�� ( )
���ij�ֱ�Ҫ�l���Ă�(g��)��(sh��)�� ( )
��![]() �� ��
�� ��![]() �� ��
�� ��![]() ��
��
��![]() �� ��
�� ��![]() �� ��
�� ��![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ķքe����1,2,3,4��4����Ƭ���S�C(j��)��ȡ1�����Żغ����S�C(j��)��ȡ1�����t��õĵ�һ����Ƭ�ϵĔ�(sh��)���ڵڶ�����Ƭ�ϵĔ�(sh��)�ĸ��ʞ飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���Ї�(gu��)�Ŵ��еġ��Y����(l��)���䡢����������(sh��)���ϷQ����ˇ��.���Y������Ҫָ����������(l��)������Ҫָ���������䡱�͡������������w���̈́ڄ�(d��ng)����������ָ���N�vʷ�Ļ�֪�R(sh��)������(sh��)����ָ��(sh��)�W(xu��).ijУ��(gu��)�W(xu��)��F(tu��n)�_չ����ˇ���n���v�����(d��ng)��ÿˇ����һ��(ji��)���B������(ji��)��һ���n���v�����n������Ҫ����(sh��)��������ڵ�����(ji��)���ҡ��䡱�͡��������T�n���������n���t����ˇ���n���v����ͬ�����n����У� ��
A.12�NB.24�NC.36�ND.48�N
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com