【題目】已知,函數
其中
（1）討論函數
的單調性；
（2）若函數有兩個零點，
(i)求
的取值范圍；
(ii)設的兩個零點分別為x1,x2，證明：x1x2>e2．
【答案】（1）見解析（2）(i)
；(ii)見解析
【解析】
（1）求導后，分別在
和
兩種情況下討論導函數的符號，從而得到單調區間；（2）(i)將問題轉化為
與函數
的圖象在
上有兩個不同交點，通過求解相切時的臨界值，得到
的取值范圍；(ii)將問題轉化為證明
成立，通過構造函數
，證得
，從而證得結論.
（1）函數的定義域為，
①當時，
，
在單調遞增；
②當時，由
得
，
則當
時，
，在
單調遞增；
當
時，
，在
單調遞減
（2）(i)函數有兩個零點即方程
在有兩個不同根
轉化為函數與函數的圖象在上有兩個不同交點
如圖：
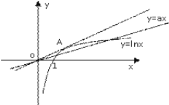
可見，若令過原點且切于函數圖象的直線斜率為
，只需
設切點
，所以
又
，所以
，解得
于是
，所以
(ii)原不等式
不妨設
，
令
，則
，于是
設函數，
求導得：
故函數
是
上的增函數 
即不等式
成立，故所證不等式
成立
科目：高中數學 來源： 題型：
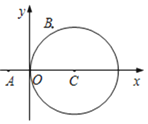
【題目】如圖，在平面直角坐標系xOy中，已知圓C：x2+y2-4x=0及點A（-1，0），B（1，2）
（1）若直線l平行于AB，與圓C相交于M，N兩點，MN=AB，求直線l的方程；
（2）若圓C上存在兩個點P，使得PA2+PB2=a（a＞4），求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系中，圓
經過伸縮變換
后得到曲線
．以坐標原點為極點，
軸的正半軸為極軸，并在兩種坐標系中取相同的單位長度，建立極坐標系，直線
的極坐標方程為
．
（1）求曲線的直角坐標方程及直線的直角坐標方程；
（2）設點
是上一動點，求點到直線的距離的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】判斷下列命題的真假：
（1）
是
的必要條件；
（2）
是
的充要條件；
（3）兩個三角形的兩組對應角相等是這兩個三角形相似的充要條件；
（4）三角形的三條邊滿足勾股定理是這個三角形為直角三角形的充要條件；
（5）在
中，重心和垂心重合是為等邊三角形的必要條件；
（6）如果點
到點
的距離相等，則點一定在線段
的垂直平分線上.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某同學用“五點法”畫函數f(x)=Asin(ωx+
)(A>0，ω>0，||<
)在某一個周期內的圖象時，列表并填入了部分數據，如表：
ωx+ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+ | 0 | 5 | -5 | 0 |
（1）請將上表數據補充完整，并求出函數f(x)的解析式；
（2）將y=f(x)的圖象向左平移
個單位，得到函數y=g(x)的圖象.若關于x的方程g(x)-m=0在區間[0，]上有兩個不同的解，求實數m的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】剪紙藝術是最古老的中國民間藝術之一，作為一種鏤空藝術，它能給人以視覺上以透空的感覺和藝術享受.在中國南北方的剪紙藝術，通過一把剪刀、一張紙、就可以表達生活中的各種喜怒哀樂.如圖是一邊長為1的正方形剪紙圖案，中間黑色大圓與正方形的內切圓共圓心，圓與圓之間是相切的，且中間黑色大圓的半徑是黑色小圓半徑的2倍，若在正方形圖案上隨機取一點，則該點取自白色區域的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
