圖2-1-21
(1)求證:∠1=∠2;
(2)求證:AB·AC=AE·AD;
(3)作OH⊥AB,垂足為H.求證:
.
思路分析:(1)∠1與∠2均為圓周角,要證它們相等,只需證所對的弧相等,弧BD與弧FC夾在BC與DF之間,只需證DF∥BC即可.?
(2)要證等積式,可先證比例式
=
,而這可由△ABD∽△AEC證得.?
(3)要證
,聯想到中位線定理,可先證
.
證明:(1)連結DF,∵AD為直徑,∴∠AFD =90°.?
又BC⊥AF,∴DF∥BC.?
∴ =
.∴∠1=∠2.?
(2)連結BD,∵AD為直徑,∴∠ABD =90°.?
又AE⊥BC,∴∠AEC=90°.?
∴∠ABD =∠AEC.?
又∠1=∠2,?
∴△ABD∽△AEC(或由∠1=∠2,∠ACB =∠ADB可知△ABD∽△AEC).?
∴
=
,?
即AB·AC =AE·AD.?
(3)連結CF,∵AD為直徑,∴∠ABD =90°.?
又OH⊥AB,∴OH∥BD.?
∴H為AB中點,即OH為△ABD的中位線.?
∴
.?
又
=
,∴BD =CF.?
∴
.
科目：高中數學 來源： 題型：
=3e1，
=3e2，（1）若C、D是AB的三等分點，求
、
.（用e1、e2表示）
（2）若C、D、E是AB的四等分點，求
、
、
.（用e1、e2表示）
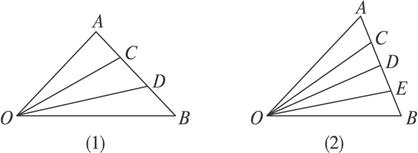
圖2-2-21
查看答案和解析>>
科目：高中數學 來源： 題型：
己知在銳角ΔABC中，角
所對的邊分別為
，且
(I )求角
大小；
(II)當
時，求
的取值范圍.
20．如圖1，在平面內，
是
的矩形，
是正三角形，將沿
折起，使
如圖2，
為的中點，設直線
過點且垂直于矩形所在平面，點
是直線上的一個動點，且與點
位于平面的同側。
（1）求證：
平面；
（2）設二面角
的平面角為
，若
，求線段
長的取值范圍。
 |
21.已知A，B是橢圓
的左，右頂點，
，過橢圓C的右焦點F的直線交橢圓于點M，N，交直線
于點P，且直線PA，PF，PB的斜率成等差數列,R和Q是橢圓上的兩動點，R和Q的橫坐標之和為2，RQ的中垂線交X軸于T點
(1)求橢圓C的方程；
（2）求三角形MNT的面積的最大值
22. 已知函數
，
（Ⅰ）若
在
上存在最大值與最小值，且其最大值與最小值的和為
，試求
和
的值。
（Ⅱ）若為奇函數：
（1）是否存在實數，使得在
為增函數，
為減函數，若存在，求出的值，若不存在，請說明理由；
（2）如果當
時，都有
恒成立，試求的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
（12分）評委會把同學們上交的作品的件數按5天一組分組統計，繪制了頻率分布直方 圖，如圖所示，已知從左到右各長方形的高的比為2:3:4:6:4:1,第三組的頻數為 12 ，請解答下列問題：（1）本次活動共有多少件作品參加評比？
（2）那組上交的作品量最多？有多少件？
（3）經過評比，第四組和第六組分別有10件、2件作品獲獎，問這兩組哪組的獲獎率高？
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
如圖所示，已知在△ABC中，∠C=90°，正方形DEFC內接于△ABC，DE∥AC，EF∥BC，AC=1，BC=2，則AF：FC=