如圖,△OBC的在個頂點坐標(biāo)分別為(0,0)、(1,0)、(0,2),設(shè)P為線段BC的中點,P為線段CO的中點,P3為線段OP1的中點,對于每一個正整數(shù)n,Pn+3為線段PnPn+1的中點,令Pn的坐標(biāo)為(xn,yn),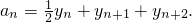
(Ⅰ)求a1,a2,a3及an;
(Ⅱ)證明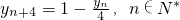 ;
;
(Ⅲ)若記bn=y4n+4-y4n,n∈N*,證明{bn}是等比數(shù)列.
解:(Ⅰ)因為
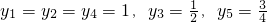
,
所以a
1=a
2=a
3=2,又由題意可知
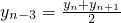
∴
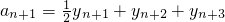
=
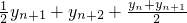
=
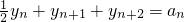
,
∴{a
n}為常數(shù)列
∴a
n=a
1=2,n∈N
*.
(Ⅱ)將等式
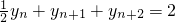
兩邊除以2,得
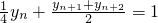
,
又∵

∴
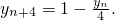
(Ⅲ)∵
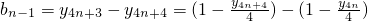
=
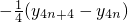
=
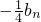
,
又∵
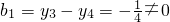
,
∴{b
n}是公比為

的等比數(shù)列.
分析:(Ⅰ)由題意可知
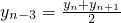
,由此可推導(dǎo)出a
n=a
1=2,n∈N
*.
(Ⅱ)將等式
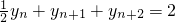
兩邊除以2,得
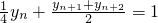
,由此可知
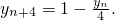
(Ⅲ)由
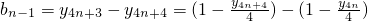
=
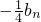
和
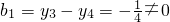
,知{b
n}是公比為

的等比數(shù)列.
點評:本題考查數(shù)列的性質(zhì)和綜合運(yùn)用,解題時要注意公式的靈活運(yùn)用.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
如圖,△OBC的在個頂點坐標(biāo)分別為(0,0)、(1,0)、(0,2),設(shè)P為線段BC的中點,P為線段CO的中點,P
3為線段OP
1的中點,對于每一個正整數(shù)n,P
n+3為線段P
nP
n+1的中點,令P
n的坐標(biāo)為(x
n,y
n),
an=yn+yn+1+yn+2.(Ⅰ)求a
1,a
2,a
3及a
n;
(Ⅱ)證明
yn+4=1-,n∈N*;
(Ⅲ)若記b
n=y
4n+4-y
4n,n∈N
*,證明{b
n}是等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:數(shù)學(xué)教研室
題型:044
如圖,ΔOBC的在個頂點坐標(biāo)分別為(0,0)、(1,0)、(0,2),設(shè)P為線段BC的中點,P2為線段CO的中點,P3為線段OP1的中點,對于每一個正整數(shù)n,Pn+3為線段PnPn+1的中點,令Pn的坐標(biāo)為(xn,yn), 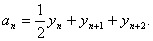
(Ⅰ)求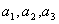 及
及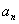 ;
;
(Ⅱ)證明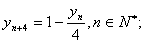
(Ⅲ)若記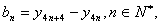 證明
證明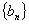 是等比數(shù)列.
是等比數(shù)列.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,△OBC的在個頂點坐標(biāo)分別為(0,0)、(1,0)、(0,2),設(shè)P為線段BC的中點,P為線段CO的中點,P
3為線段OP
1的中點,對于每一個正整數(shù)n,P
n+3為線段P
nP
n+1的中點,令P
n的坐標(biāo)為(x
n,y
n),
an=yn+yn+1+yn+2.(Ⅰ)求a
1,a
2,a
3及a
n;
(Ⅱ)證明
yn+4=1-,n∈N*;
(Ⅲ)若記b
n=y
4n+4-y
4n,n∈N
*,證明{b
n}是等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2004年浙江省高考數(shù)學(xué)試卷(理科)(解析版)
題型:解答題
如圖,△OBC的在個頂點坐標(biāo)分別為(0,0)、(1,0)、(0,2),設(shè)P為線段BC的中點,P為線段CO的中點,P
3為線段OP
1的中點,對于每一個正整數(shù)n,P
n+3為線段P
nP
n+1的中點,令P
n的坐標(biāo)為(x
n,y
n),
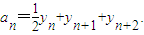
(Ⅰ)求a
1,a
2,a
3及a
n;
(Ⅱ)證明
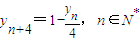
;
(Ⅲ)若記b
n=y
4n+4-y
4n,n∈N
*,證明{b
n}是等比數(shù)列.
查看答案和解析>>

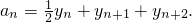
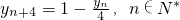 ;
; 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案![]() 及
及![]() ;
;![]()
![]() 證明
證明![]() 是等比數(shù)列.
是等比數(shù)列.
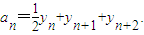
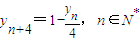 ;
;