Question

F₁、F₂是橢圓的兩個焦點，M是橢圓上任一點，從任一焦點向△F₁MF₂頂點M的外角平分線引垂線，垂足為P，則P點的軌跡為（ ）
A．圓
B．橢圓
C．雙曲線
D．拋物線

Answer 1

【答案】分析：根據題意，延長F₁P，與F₂M的延長線交于B點，連接PO．根據等腰三角形“三線合一”和三角形中位線定理，結合橢圓的定義證出OP的長恰好等于橢圓的長半軸a，得動點P的軌跡方程為x²+y²=a²，由此可得本題答案．
解答：解：如圖所示
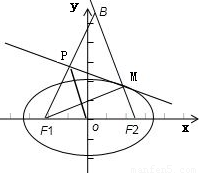
延長F₁P，與F₂M的延長線交于B點，連接PO，
∵MP是∠F₁MB的平分線，且PM⊥BF₁
∴△F₁MB中，|MF₁|=|BM|且P為BF₁的中點
由三角形中位線定理，得|OP|=|BF₂|=（|BM|+|MF₂|）
∵由橢圓的定義，得|MF₁|+|MF₂|=2a，（2a是橢圓的長軸）
可得|BM|+|MF₂|=2a，
∴|OP|=（|MF₁|+|MF₂|）=a，可得動點P的軌跡方程為x²+y²=a²
為以原點為圓心半徑為a的圓
故選：A
點評：本題在橢圓中求動點P的軌跡，著重考查了橢圓的定義、等腰三角形的判定和三角形中位線定理等知識，屬于中檔題．