
【題目】德國數學家科拉茨![]() 年提出了一個著名的猜想:任給一個正整數
年提出了一個著名的猜想:任給一個正整數![]() ,如果
,如果![]() 是偶數,就將它減半(即
是偶數,就將它減半(即![]() );如果
);如果![]() 是奇數,則將它乘
是奇數,則將它乘![]() 加
加![]() (即
(即![]() ),不斷重復這樣的運算,經過有限步后,一定可以得到
),不斷重復這樣的運算,經過有限步后,一定可以得到![]() .對于科拉茨猜想,目前誰也不能證明,也不能否定.現在請你研究:如果對正整數
.對于科拉茨猜想,目前誰也不能證明,也不能否定.現在請你研究:如果對正整數![]() (首項)按照上述規則施行變換后的第
(首項)按照上述規則施行變換后的第![]() 項為
項為![]() (注:
(注:![]() 可以多次出現),則
可以多次出現),則![]() 的所有不同值的個數為( )
的所有不同值的個數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:
【題目】如圖是一個半圓形湖面景點的平面示意圖.已知![]() 為直徑,且
為直徑,且![]() km,
km,![]() 為圓心,
為圓心,![]() 為圓周上靠近
為圓周上靠近![]() 的一點,
的一點,![]() 為圓周上靠近
為圓周上靠近![]() 的一點,且
的一點,且![]() ∥
∥![]() .現在準備從
.現在準備從![]() 經過
經過![]() 到
到![]() 建造一條觀光路線,其中
建造一條觀光路線,其中![]() 到
到![]() 是圓弧
是圓弧![]() ,
,![]() 到
到![]() 是線段
是線段![]() .設
.設![]() ,觀光路線總長為
,觀光路線總長為![]() .
.

(1)求![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)求觀光路線總長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是橢圓
是橢圓![]() :
:![]() 的左、右焦點,
的左、右焦點,![]() 恰好與拋物線
恰好與拋物線![]() 的焦點重合,過橢圓
的焦點重合,過橢圓![]() 的左焦點
的左焦點![]() 且與
且與![]() 軸垂直的直線被橢圓
軸垂直的直線被橢圓![]() 截得的線段長為3.
截得的線段長為3.
(1)求橢圓![]() 的方程;
的方程;
(2)已知點![]() ,直線
,直線![]() :
:![]() ,過
,過![]() 斜率為
斜率為![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,與直線
兩點,與直線![]() 交于
交于![]() 點,若直線
點,若直線![]() ,
,![]() ,
,![]() 的斜率分別是
的斜率分別是![]() ,
,![]() ,
,![]() ,求證:無論
,求證:無論![]() 取何值,總滿足
取何值,總滿足![]() 是
是![]() 和
和![]() 的等差中項.
的等差中項.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】a,b為空間中兩條互相垂直的直線,等腰直角三角形ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉軸旋轉,有下列結論:
①當直線AB與a成60°角時,AB與b成30°角;
②當直線AB與a成60°角時,AB與b成60°角;
③直線AB與a所成角的最小值為45°;
④直線AB與a所成角的最大值為60°.
其中正確的是________.(填寫所有正確結論的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A4紙是生活中最常用的紙規格.A系列的紙張規格特色在于:①A0、A1、A2…、A5,所有尺寸的紙張長寬比都相同.②在A系列紙中,前一個序號的紙張以兩條長邊中點連線為折線對折裁剪分開后,可以得到兩張后面序號大小的紙,比如1張A0紙對裁后可以得到2張A1紙,1張A1紙對裁可以得到2張A2紙,依此類推.這是因為A系列紙張的長寬比為![]() :1這一特殊比例,所以具備這種特性.已知A0紙規格為84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1這一特殊比例,所以具備這種特性.已知A0紙規格為84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4紙的長度為( )
,那么A4紙的長度為( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
以平面直角坐標系![]() 的原點為極點,
的原點為極點, ![]() 軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位,直線
軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),圓
為參數),圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與圓
的普通方程與圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于
交于![]() 兩點,若
兩點,若![]() 點的直角坐標為
點的直角坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過研究學生的學習行為,心理學家發現,學生接受能力依賴于老師引入概念和描述問題所用的時間,講座開始時,學生的興趣激增,中間有一段不太長的時間,學生的興趣保持理想的狀態,隨后學生的注意力開始分散.分析結果和實驗表明,用![]() 表示學生掌握和接收概念的能力(
表示學生掌握和接收概念的能力(![]() 的值越大,表示接受能力越強),
的值越大,表示接受能力越強),![]() 表示提出和講授概念的時間(單位:分鐘),可以有以下公式:
表示提出和講授概念的時間(單位:分鐘),可以有以下公式: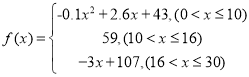
(1)開講多少分鐘后,學生的接受能力最強?能維持多長時間?
(2)開講5分鐘與開講20分鐘比較,學生的接受能力何時強一些?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com