
【題目】如圖是一個半圓形湖面景點的平面示意圖.已知![]() 為直徑,且
為直徑,且![]() km,
km,![]() 為圓心,
為圓心,![]() 為圓周上靠近
為圓周上靠近![]() 的一點,
的一點,![]() 為圓周上靠近
為圓周上靠近![]() 的一點,且
的一點,且![]() ∥
∥![]() .現在準備從
.現在準備從![]() 經過
經過![]() 到
到![]() 建造一條觀光路線,其中
建造一條觀光路線,其中![]() 到
到![]() 是圓弧
是圓弧![]() ,
,![]() 到
到![]() 是線段
是線段![]() .設
.設![]() ,觀光路線總長為
,觀光路線總長為![]() .
.

(1)求![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)求觀光路線總長的最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
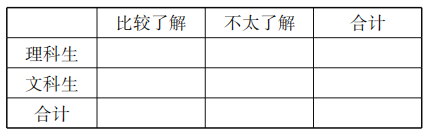
【題目】阿基米德是古希臘偉大的哲學家、數學家、物理學家,對幾何學、力學等學科作出過卓越貢獻.為調查中學生對這一偉大科學家的了解程度,某調查小組隨機抽取了某市的100名高中生,請他們列舉阿基米德的成就,把能列舉阿基米德成就不少于3項的稱為“比較了解”,少于三項的稱為“不太了解”他們的調查結果如下:

(1)完成如下![]() 列聯表,并判斷是否有99%的把握認為,了解阿基米德與選擇文理科有關?
列聯表,并判斷是否有99%的把握認為,了解阿基米德與選擇文理科有關?
(2)在抽取的100名高中生中,按照文理科采用分層抽樣的方法抽取10人的樣本.
(ⅰ)求抽取的文科生和理科生的人數;
(ⅱ)從10人的樣本中隨機抽取3人,用![]() 表示這3人中文科生的人數,求
表示這3人中文科生的人數,求![]() 的分布列和數學期望.參考數據:
的分布列和數學期望.參考數據:

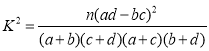 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg), 其頻率分布直方圖如下:

(1)記A表示事件“舊養殖法的箱產量低于50 kg”,估計A的概率;
(2)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關:
箱產量<50 kg | 箱產量≥50 kg | |
舊養殖法 | ||
新養殖法 |
(3)根據箱產量的頻率分布直方圖,對這兩種養殖方法的優劣進行比較.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學專著《九章算術》中有一個“兩鼠穿墻題”,其內容為:“今有垣厚五尺,兩鼠對穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半.問何日相逢?各穿幾何?”如圖的程序框圖源于這個題目,執行該程序框圖,若輸入x=20,則輸出的結果為( )
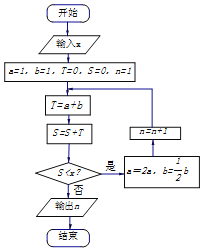
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (φ為參數),在以O為極點,x軸的正半軸為極軸的極坐標系中,曲線C2是圓心為(2,
(φ為參數),在以O為極點,x軸的正半軸為極軸的極坐標系中,曲線C2是圓心為(2,![]() ),半徑為1的圓.
),半徑為1的圓.
(1)求曲線C1的普通方程和C2的直角坐標方程;
(2)設M為曲線C1上的點,N為曲線C2上的點,求|MN|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 與直線
與直線![]() 交于
交于![]() 不同兩點分別過點
不同兩點分別過點![]() 、點
、點![]() 作拋物線
作拋物線![]() 的切線,所得的兩條切線相交于點
的切線,所得的兩條切線相交于點![]() .
.
(Ⅰ)求證![]() 為定值:
為定值:
(Ⅱ)求![]() 的面積的最小值及此時的直線
的面積的最小值及此時的直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記![]() 為數列
為數列![]() 的前
的前![]() 項和.“任意正整數
項和.“任意正整數![]() ,均有
,均有![]() ”是“
”是“![]() 為遞增數列”的
為遞增數列”的
A. 充分不必要條件 B. 必要不充分條件
C. 充要條件 D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國數學家科拉茨![]() 年提出了一個著名的猜想:任給一個正整數
年提出了一個著名的猜想:任給一個正整數![]() ,如果
,如果![]() 是偶數,就將它減半(即
是偶數,就將它減半(即![]() );如果
);如果![]() 是奇數,則將它乘
是奇數,則將它乘![]() 加
加![]() (即
(即![]() ),不斷重復這樣的運算,經過有限步后,一定可以得到
),不斷重復這樣的運算,經過有限步后,一定可以得到![]() .對于科拉茨猜想,目前誰也不能證明,也不能否定.現在請你研究:如果對正整數
.對于科拉茨猜想,目前誰也不能證明,也不能否定.現在請你研究:如果對正整數![]() (首項)按照上述規則施行變換后的第
(首項)按照上述規則施行變換后的第![]() 項為
項為![]() (注:
(注:![]() 可以多次出現),則
可以多次出現),則![]() 的所有不同值的個數為( )
的所有不同值的個數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com