
【題目】2020年1月10日,引發新冠肺炎疫情的COVID-9病毒基因序列公布后,科學家們便開始了病毒疫苗的研究過程.但是類似這種病毒疫苗的研制需要科學的流程,不是一朝一夕能完成的,其中有一步就是做動物試驗.已知一個科研團隊用小白鼠做接種試驗,檢測接種疫苗后是否出現抗體.試驗設計是:每天接種一次,3天為一個接種周期.已知小白鼠接種后當天出現抗體的概率為![]() ,假設每次接種后當天是否出現抗體與上次接種無關.
,假設每次接種后當天是否出現抗體與上次接種無關.
(1)求一個接種周期內出現抗體次數![]() 的分布列;
的分布列;
(2)已知每天接種一次花費100元,現有以下兩種試驗方案:
①若在一個接種周期內連續2次出現抗體即終止本周期試驗,進行下一接種周期,試驗持續三個接種周期,設此種試驗方式的花費為![]() 元;
元;
②若在一個接種周期內出現2次或3次抗體,該周期結束后終止試驗,已知試驗至多持續三個接種周期,設此種試驗方式的花費為![]() 元.
元.
比較隨機變量![]() 和
和![]() 的數學期望的大小.
的數學期望的大小.
科目:高中數學 來源: 題型:
【題目】如圖,直角梯形![]() 與等腰直角三角形
與等腰直角三角形![]() 所在的平面互相垂直.
所在的平面互相垂直.![]()
![]() ,
,![]() ,
,![]() .
.
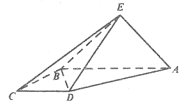
(1)求證:![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(文)(2017·衡水二模)某商場在元旦舉行購物抽獎促銷活動,規定顧客從裝有編號0,1,2,3,4的五個相同小球的抽獎箱中一次任意摸出兩個小球,若取出的兩個小球的編號之和等于7則中一等獎,等于6或5則中二等獎,等于4則中三等獎,其余結果為不中獎.
(1)求中二等獎的概率.
(2)求不中獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
B. 命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. “![]() 在
在![]() 處有極值”是“
處有極值”是“![]() ”的充要條件
”的充要條件
D. 命題“若函數![]() 有零點,則“
有零點,則“![]() 或
或![]() ”的逆否命題為真命題
”的逆否命題為真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰![]() 中,斜邊
中,斜邊![]() ,
,![]() 為直角邊
為直角邊![]() 上的一點,將
上的一點,將![]() 沿直線
沿直線![]() 折疊至
折疊至![]() 的位置,使得點
的位置,使得點![]() 在平面
在平面![]() 外,且點
外,且點![]() 在平面
在平面![]() 上的射影
上的射影![]() 在線段
在線段![]() 上設
上設![]() ,則
,則![]() 的取值范圍是( )
的取值范圍是( )
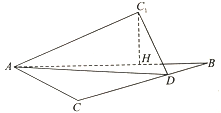
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com