
【題目】已知直三棱柱![]() 的底面是邊長為6的等邊三角形,
的底面是邊長為6的等邊三角形,![]() 是
是![]() 邊上的中點,
邊上的中點,![]() 點滿足
點滿足![]() ,平面
,平面![]() 平面
平面![]() ,求:
,求:
(1)側棱長;
(2)直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
科目:高中數學 來源: 題型:
【題目】容器中有![]()
![]() 種粒子,若相同種類的兩顆粒子發生碰撞,則變成一顆
種粒子,若相同種類的兩顆粒子發生碰撞,則變成一顆![]() 粒子;不同種類的兩顆粒子發生碰撞,會變成另外一種粒子. 例如,一顆
粒子;不同種類的兩顆粒子發生碰撞,會變成另外一種粒子. 例如,一顆![]() 粒子和一顆
粒子和一顆![]() 粒子發生碰撞則變成一顆
粒子發生碰撞則變成一顆![]() 粒子.現有
粒子.現有![]() 粒子
粒子![]() 顆,
顆,![]() 粒子
粒子![]() 顆,
顆,![]() 粒子
粒子![]() 顆,如果經過各種兩兩碰撞后,只剩
顆,如果經過各種兩兩碰撞后,只剩![]() 顆粒子. 給出下列結論:
顆粒子. 給出下列結論:
① 最后一顆粒子可能是![]() 粒子
粒子
② 最后一顆粒子一定是![]() 粒子
粒子
③ 最后一顆粒子一定不是![]() 粒子
粒子
④ 以上都不正確
其中正確結論的序號是________.(寫出所有正確結論的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線C的極坐標方程為ρ﹣4cosθ+3ρsin2θ=0,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,直線l過點M(1,0),傾斜角為![]() .
.
(Ⅰ)求曲線C的直角坐標方程與直線l的參數方程;
(Ⅱ)若曲線C經過伸縮變換![]() 后得到曲線C′,且直線l與曲線C′交于A,B兩點,求|MA|+|MB|.
后得到曲線C′,且直線l與曲線C′交于A,B兩點,求|MA|+|MB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】二次函數![]() 的圖象頂點為
的圖象頂點為![]() ,且圖象在
,且圖象在![]() 軸上截得的線段長為8.
軸上截得的線段長為8.
(1)求函數![]() 的解析式;
的解析式;
(2)令![]() .
.
(ⅰ)求函數![]() 在
在![]() 上的最小值;
上的最小值;
(ⅱ)若![]() 時,不等式
時,不等式![]() 恒成立,試求實數
恒成立,試求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】總體由編號為01,02,03,![]() ,49,50的50個個體組成,利用隨機數表(以下選取了隨機數表中的第1行和第2行)選取5個個體,選取方法是從隨機數表第1行的第9列和第10列數字開始由左向右讀取,則選出來的第4個個體的編號為( )
,49,50的50個個體組成,利用隨機數表(以下選取了隨機數表中的第1行和第2行)選取5個個體,選取方法是從隨機數表第1行的第9列和第10列數字開始由左向右讀取,則選出來的第4個個體的編號為( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex-e-x(x∈R且e為自然對數的底數).
(1)判斷函數f(x)的奇偶性與單調性.
(2)解關于t不等式f(x-t)+f(x2-2t)≥0對一切實數x都成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD⊥平面PCD,PD⊥CD,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2AB, ![]() 為棱PC上一點.
為棱PC上一點.
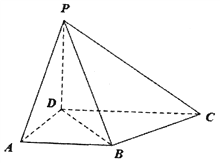
(Ⅰ)若點![]() 是PC的中點,證明:B
是PC的中點,證明:B![]() ∥平面PAD;
∥平面PAD;
(Ⅱ) ![]() 試確定
試確定![]() 的值使得二面角
的值使得二面角![]() -BD-P為60°.
-BD-P為60°.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com