Question

15．已知P為函數$y=\frac{1}{4}{x^2}$圖象上一動點，過點P做x軸的垂線，垂足為B，已知A（3，2），則|PA|+|PB|的最小值為（　　）

• A． $\sqrt{5}+\sqrt{2}$
• B． $\sqrt{10}-1$
• C． $2\sqrt{3}+2$
• D． $3\sqrt{5}-2$

Answer 1

分析 根據拋物線方程得到拋物線焦點為F，并且作出它的準線：x=-1，延長PB交準線于點C，連接PF、AF，根據拋物線的定義可得得：|PA|+|PB|=|PA|+|PC|-1=|PA|+|PF|-1．再由三角形兩邊之和大于第三邊可得：P點滿足|PA|+|PF|≥|AF|，當且僅當點P落在線段AF上時，|PA|+|PF|=|AF|為最小值，最后根據兩點的距離公式得到|PA|+|PF|的最小值，然后求解即可．

解答 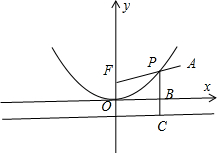解：∵函數$y=\frac{1}{4}{x^2}$，即拋物線方程為x²=4y，
∴拋物線的焦點為F（0，1），準線為y=-1，延長P，B交準線于點C，連接PF、AF，根據拋物線的定義得：|PF|=|PC|
∴|PA|+|PB|=|PA|+|PC|-1=|PA|+|PF|-1，當P點不在AF上時，
有|PA|+|PF|＞|AF|；
當P點剛好落在AF上時，有|PA|+|PF|=|AF|，
∴P點滿足|PA|+|PF|≥|AF|，
當且僅當點P落在線段AF上時，|PA|+|PF|=|AF|為最小值，
所以|PA|+|PF|的最小值為$\sqrt{{3}^{2}+（2-1）^{2}}$=$\sqrt{10}$，
同時|PA|+|PM|的最小值是|PA|+|PC|-1=|PA|+|PF|-1=$\sqrt{10}-1$
故選：B．

點評 本題給出拋物線上一個動點P在y軸上的射影點為M，求點P到B點和A的距離之和的最小值，著重考查了拋物線的定義和簡單幾何性質和兩點間的距離公式等知識點，屬于中檔題．