
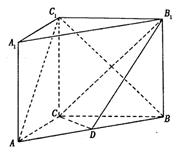
如圖,直三棱柱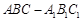 中,
中,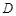 、
、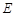 分別是棱
分別是棱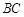 、
、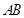 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)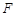 在棱
在棱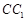 上,已知
上,已知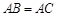 ,
,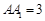 ,
,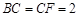 .
.
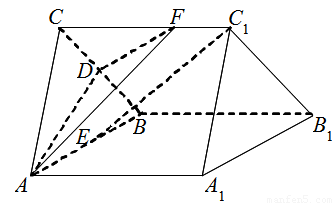
(1)求證: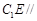 平面
平面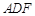 ;
;
(2)設(shè)點(diǎn)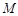 在棱
在棱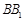 上,當(dāng)
上,當(dāng)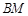 為何值時(shí),平面
為何值時(shí),平面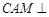 平面
平面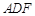 ?
?
(1)詳見解析;(2)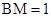
【解析】

試題分析:(1)要證明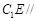 平面
平面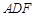 ,只需在平面內(nèi)找一條直線與
,只需在平面內(nèi)找一條直線與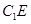 平行,如果不容易直接找到,可以將
平行,如果不容易直接找到,可以將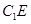 平移到平面內(nèi),平移直線的方法一般有①中位線平移;②平行四邊形對邊平行平移;③成比例線段平移,該題連接
平移到平面內(nèi),平移直線的方法一般有①中位線平移;②平行四邊形對邊平行平移;③成比例線段平移,該題連接 交
交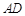 于
于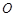 ,連接
,連接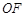 ,可證
,可證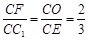 ,從而
,從而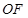 ∥
∥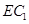 ,進(jìn)而可證
,進(jìn)而可證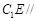 平面
平面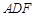 ;(2)該題主要是如何分析得到
;(2)該題主要是如何分析得到 的位置,然后再證明,由已知可得平面
的位置,然后再證明,由已知可得平面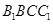
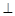 平面
平面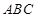 ,進(jìn)而可證
,進(jìn)而可證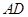
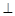 平面
平面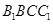 ,故AD
,故AD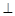 CM,只需有
CM,只需有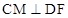 ,則CM
,則CM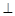 平面
平面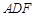 ,從而平面
,從而平面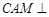 平面
平面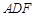 ,那么如何保證
,那么如何保證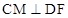 呢?在矩形
呢?在矩形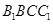 中,只需
中,只需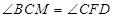 ,則
,則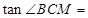
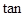
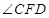 ,則
,則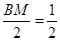 ,所以
,所以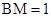 ,倒過來,再證明平面
,倒過來,再證明平面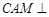 平面
平面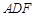 即可.
即可.
試題解析:(1)連接 交
交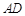 于
于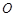 ,連接
,連接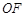 ,因?yàn)镃E,AD為△ABC中線,所以O(shè)為△ABC的重心,
,因?yàn)镃E,AD為△ABC中線,所以O(shè)為△ABC的重心,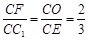 ,從而OF//C1E,OF
,從而OF//C1E,OF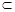 面ADF,
面ADF,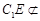 平面
平面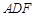 ,所以
,所以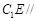 平面
平面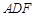 ;
;
(2)當(dāng)BM=1時(shí),平面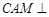 平面
平面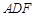 .
.
在直三棱柱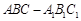 中,由于
中,由于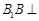 平面ABC,BB1
平面ABC,BB1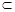 平面B1BCC1,所以平面B1BCC1
平面B1BCC1,所以平面B1BCC1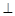 平面ABC,由于AB=AC,
平面ABC,由于AB=AC,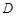 是
是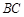 中點(diǎn),所以
中點(diǎn),所以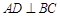 ,又平面B1BCC1∩平面ABC=BC,所以AD
,又平面B1BCC1∩平面ABC=BC,所以AD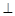 平面B1BCC1,
而CM
平面B1BCC1,
而CM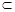 平面B1BCC1,于是AD
平面B1BCC1,于是AD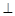 CM,因?yàn)锽M =CD=1,BC= CF=2,所以
CM,因?yàn)锽M =CD=1,BC= CF=2,所以 ≌
≌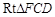 ,所CM
,所CM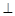 DF,
DF,
DF與AD相交,所以CM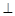 平面
平面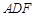 ,CM
,CM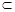 平面CAM,所以平面
平面CAM,所以平面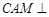 平面
平面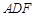 ,∴當(dāng)BM=1時(shí),平面
,∴當(dāng)BM=1時(shí),平面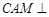 平面
平面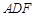 .
.
考點(diǎn):1、直線和平面平行的判定;2、面面垂直的判定;3、面面垂直的性質(zhì).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(09年東城區(qū)期末理)(14分)
如圖,在直三棱柱![]() 中,
中,![]() .
.
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() ∥平面
∥平面![]() ,若存在,試給出證明;若不存在,請說明理由.
,若存在,試給出證明;若不存在,請說明理由.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆天津市高二第一次月考數(shù)學(xué)試卷(解析版) 題型:解答題
(13分) 如圖,直三棱柱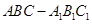 中,
中,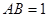 ,
,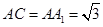 ,
,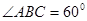 .
.
(Ⅰ)證明: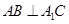 ;
;
(Ⅱ)求二面角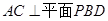
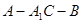 的正切值.
的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年四川省高三9月月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
如圖,直三棱柱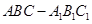 中,
中,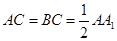 ,
,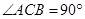 ,
,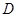 是棱
是棱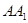 的中點(diǎn).
的中點(diǎn).
(Ⅰ)證明: ;
;
(Ⅱ)求二面角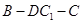 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆廣東惠陽一中實(shí)驗(yàn)學(xué)校高二6月月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分14分)如圖, 在直三棱柱 中,
中,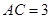 ,
,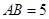 ,
,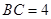
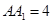 ,點(diǎn)
,點(diǎn)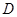 是
是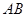 的中點(diǎn).
的中點(diǎn).
⑴求證: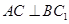 ;
;
⑵求證: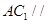 平面
平面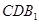 ;
;
⑶求二面角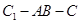 的正切值.
的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆天津市等三校高二第一學(xué)期期末聯(lián)合考試文科數(shù)學(xué)試卷 題型:解答題
如圖, 在直三棱柱 中,
中, ,
, ,點(diǎn)
,點(diǎn) 是
是 的中點(diǎn),
的中點(diǎn),
(1)求證: ;
;
(2)求證: ;
;
(3)求直線 與平面
與平面 所成角的正切值.
所成角的正切值.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com