C
分析:由sinA:sinB:sinC=7:8:13,利用正弦定理得到三角形三邊之比,設出三角形的三邊,利用余弦定理表示出cosC,化簡后得到cosC的值,由C的范圍,利用特殊角的三角函數值即可求出角C的大小.
解答:由正弦定理得:

=

=

,又sinA:sinB:sinC=7:8:13,
所以a:b:c=7:8:13,設a=7k,b=8k,c=13k(k>0),
則cosC=

=
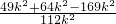
=-

,又C∈(0,π),
所以角C的大小為:120°.
故選C
點評:此題考查學生靈活運用正弦、余弦定理化簡求值,牢記特殊角的三角函數值,是一道中檔題.本題的關鍵是根據比例設出三角形的三邊.
