
為了了解某市工廠開展群眾體育活動的情況,擬采用分層抽樣的方法從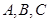 三個區中抽取6個工廠進行調查.已知
三個區中抽取6個工廠進行調查.已知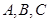 區中分別有27,18,9個工廠.
區中分別有27,18,9個工廠.
(Ⅰ)求從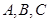 區中應分別抽取的工廠個數;
區中應分別抽取的工廠個數;
(Ⅱ)若從抽得的6個工廠中隨機地抽取2個進行調查結果的對比,求這2個工廠中至少有1個來自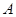 區的概率.
區的概率.
(Ⅰ)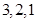 ;(Ⅱ)
;(Ⅱ)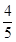
【解析】
試題分析:(Ⅰ)由分層抽樣的含義即可得總共有54個工廠,所以抽取的6個工廠占總數的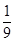 ,所以每個區域的工廠的個數即可求出.
,所以每個區域的工廠的個數即可求出.
(Ⅱ)因為6個被抽到的工廠中,A區有3個工廠,B區有2個,C區有1個.從中抽取兩個工廠共有15種情況,一一列舉出來.通過數2個工廠中都沒來自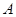 區的共有3種情況,所以符合2個工廠中至少有1個來自
區的共有3種情況,所以符合2個工廠中至少有1個來自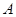 區的共有12種,即可求得結論.
區的共有12種,即可求得結論.
試題解析:解:(Ⅰ)由題可知,每個個體被抽取到得概率為 ;
;
設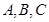 三個區被抽到的工廠個數為
三個區被抽到的工廠個數為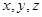 ,則
,則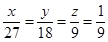
所以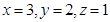 ,故
,故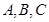 三個區被抽到的工廠個數分別為
三個區被抽到的工廠個數分別為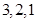
(Ⅱ)設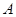 區抽到的工廠為
區抽到的工廠為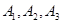 ,
,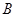 區抽到的工廠為
區抽到的工廠為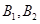 ,
,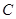 區抽到的工廠為
區抽到的工廠為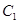
則從6間工廠抽取2個工廠,基本事件有: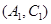 ,
,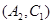 ,
,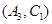 ,
,
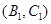 ,
,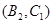 ,
,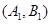 ,
,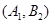 ,
,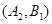 ,
,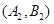 ,
,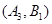 ,
,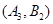
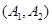 ,
,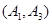 ,
, ,
,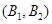 共15種情況;
共15種情況;
2個都沒來自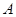 區的基本事件有
區的基本事件有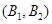 ,
,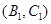 ,
,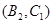 共3種情況
共3種情況
設事件“至少一個工廠來自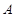 區”為事件
區”為事件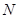 ,則事件
,則事件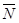 為“2個都沒來自
為“2個都沒來自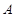 區”
區”
所以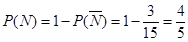
所以,至少有一個工廠來自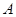 區的概率為
區的概率為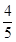
考點:1.分層抽樣的思想.2.概率的計算中含至少通常考慮從對立面出發.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三下學期開學考試文科數學 題型:解答題
為了了解某市工廠開展群眾體育活動的情況,擬采用分層抽樣的方法從A、B、C三個區中抽取6個工廠進行調查.已知A、B、C區中分別有18,27,9個工廠.
(1)求從A、B、C區中應分別抽取的工廠個數;
(2)若從抽得的6個工廠中隨機地抽取2個進行調查結果的對比,求這2個工廠中至少有1個來自A區的概率。
查看答案和解析>>
科目:高中數學 來源:2013屆江西省高二下學期第二次月考文科數學試卷 題型:解答題
為了了解某市工廠開展群眾體育活動的情況,擬采用分層抽樣的方法從A、B、C三個區中抽取6個工廠進行調查.已知A、B、C區中分別有18, 27,9個工廠.
(1)求從A、B、C區中應分別抽取的工廠個數;
(2)若從抽得的6個工廠中隨機地抽取2個進行調查結果的對比,求這2個工廠中至少有1個來自A區的概率。
查看答案和解析>>
科目:高中數學 來源:廣州省2009-2010學年高一學科競賽 題型:解答題
為了了解某市工廠開展群眾體育活動的情況,擬采用分層抽樣的方法從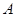 、
、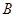 、
、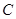 三個區中抽取7個工廠進行調查,已知
三個區中抽取7個工廠進行調查,已知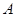 、
、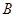 、
、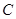 區中分別有18、27、18個工廠。
區中分別有18、27、18個工廠。
(1)求從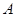 、
、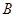 、
、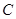 區中應分別抽取的工廠個數;
區中應分別抽取的工廠個數;
(2)若從抽得的7個工廠中隨機抽取2個進行調查結果的對比,用列舉法計算這2個工廠中至少有1個來自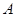 區的概率。
區的概率。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com