
【題目】已知函數![]() (
(![]() 且
且![]() 為常數).
為常數).
(1)當![]() 時,討論函數
時,討論函數![]() 在
在![]() 的單調性;
的單調性;
(2)設![]() 可求導數,且它的導函數
可求導數,且它的導函數![]() 仍可求導數,則
仍可求導數,則![]() 再次求導所得函數稱為原函數
再次求導所得函數稱為原函數![]() 的二階函數,記為
的二階函數,記為![]() ,利用二階導函數可以判斷一個函數的凹凸性.一個二階可導的函數在區間
,利用二階導函數可以判斷一個函數的凹凸性.一個二階可導的函數在區間![]() 上是凸函數的充要條件是這個函數在
上是凸函數的充要條件是這個函數在![]() 的二階導函數非負.
的二階導函數非負.
若![]() 在
在![]() 不是凸函數,求
不是凸函數,求![]() 的取值范圍.
的取值范圍.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
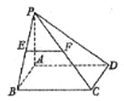
如圖,在四棱錐P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分別是PB,PC的中點.
(Ⅰ)證明:EF∥平面PAD;
(Ⅱ)求三棱錐E—ABC的體積V.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業準備投入適當的廣告費對甲產品進行促銷宣傳,在一年內預計銷量![]() (萬件)與廣告費
(萬件)與廣告費![]() (萬元)之間的函數關系為
(萬元)之間的函數關系為![]() ,已知生產此產品的年固定投入為
,已知生產此產品的年固定投入為![]() 萬元,每生產1萬件此產品仍需要再投入30萬元,且能全部銷售完,若每件甲產品銷售價格(元)定為:“平均每件甲產品生產成本的150%”與“年平均每件產品所占廣告費的50%”之和,則當廣告費為1萬元時,該企業甲產品的年利潤比不投入廣告費時的年利潤增加了__________萬元.
萬元,每生產1萬件此產品仍需要再投入30萬元,且能全部銷售完,若每件甲產品銷售價格(元)定為:“平均每件甲產品生產成本的150%”與“年平均每件產品所占廣告費的50%”之和,則當廣告費為1萬元時,該企業甲產品的年利潤比不投入廣告費時的年利潤增加了__________萬元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一般地,對于直線![]() 及直線
及直線![]() 外一點
外一點![]() ,我們有點
,我們有點![]() 到直線
到直線![]() 的距離公式為:
的距離公式為:![]() ”
”
(1)證明上述點![]() 到直線
到直線![]() 的距離公式
的距離公式
(2)設直線![]() ,試用上述公式求坐標原點
,試用上述公式求坐標原點![]() 到直線
到直線![]() 距離的最大值及取最大值時
距離的最大值及取最大值時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)的定義域為D,若存在非零實數l使得對于任意x∈M(MD),有x+l∈D,且f(x+l)![]() f(x),則稱f(x)為M上的l高調函數.現給出下列命題:①函數f(x)=2﹣x為R上的1高調函數;②函數f(x)=sin2x為R上的π高調函數;③如果定義域為[﹣1,+∞)的函數f(x)=x2為[﹣1,+∞)上m高調函數,那么實數m的取值范圍是[2,+∞);④函數f(x)=lg(|x﹣2|+1)為[1,+∞)上的2高調函數.其中真命題的個數為( )
f(x),則稱f(x)為M上的l高調函數.現給出下列命題:①函數f(x)=2﹣x為R上的1高調函數;②函數f(x)=sin2x為R上的π高調函數;③如果定義域為[﹣1,+∞)的函數f(x)=x2為[﹣1,+∞)上m高調函數,那么實數m的取值范圍是[2,+∞);④函數f(x)=lg(|x﹣2|+1)為[1,+∞)上的2高調函數.其中真命題的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要條件
”成立的充分不必要條件
B. 命題![]() ,則
,則![]()
C. 為了了解800名學生對學校某項教改試驗的意見,用系統抽樣的方法從中抽取一個容量為40的樣本,則分組的組距為40
D. 已知回歸直線的斜率的估計值為1.23,樣本點的中心為![]() ,則回歸直線方程為
,則回歸直線方程為![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com