【題目】設函數
，
，
，若
對任意
成立，且數列
滿足：
，
.
（1）求函數
的解析式；
（2）求證：
；
（3）求證：
.
【答案】（1）
；（2）（證明略）；（3）（證明略）
【解析】
（1）由題令
，解x=-1,所以-4≤f(-1)≤-4,則f(-1)=-4，得a=b-4，進而得
對任意
成立，由判別式
整理解得b=2,即可得a=-2,則f(x)可求；（2）由
得
，進而
，累乘得
（3）由（2）
得
，累加得
，再由
證明數列
遞增，得
則證得
；欲證
，即證
,則需證
，由
，放縮歸納得
，再證明
即可
（1）由題
對任意成立，
令，解x=-1,所以-4≤f(-1)≤-4,則f(-1)=-4
又
，則f(-1)=a-b=-4，即a=b-4
所以對任意成立，即
,則
整理得
∴b=2,則a=-2
所以
（2）由（1）知，
，∴, ∴
,所以
又
（3）由（2）知
所以
所以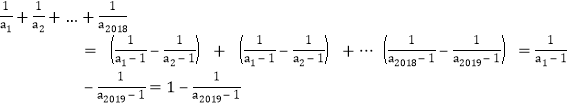
又
,又
,
為遞增數列，所以
所以
由（2）可知
，欲證，即證,則需證
∵
,∴
所以
=
所以
=2
因為2018<
所以
,則
>
所以證得，即證得
所以
考前必練系列答案科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，如圖所示，已知橢圓
的左、右頂點分別為
，
，右焦點為
.設過點
的直線
，
與此橢圓分別交于點
，
，其中
，
，
.
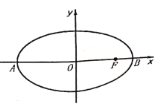
（1）設動點
滿足：
，求點的軌跡；
（2）設
，
，求點
的坐標；
（3）設
，求證：直線
必過
軸上的一定點（其坐標與
無關），并求出該定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個結論：
①命題“
，
”的否定是“
，
”；
②命題“若
，則
且
”的否定是“若，則
”；
③命題“若
，則或”的否命題是“若，則
或
”；
④若“
是假命題，
是真命題”，則命題
，
一真一假.
其中正確結論的個數為（ ）
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某旅游愛好者計劃從3個亞洲國家A1，A2，A3和3個歐洲國家B1，B2，B3中選擇2個國家去旅游.
(1)若從這6個國家中任選2個，求這2個國家都是亞洲國家的概率；
(2)若從亞洲國家和歐洲國家中各選1個，求這兩個國家包括A1，但不包括B1的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
、
、
、
是同一平面上不共線的四點，若存在一組正實數
、
、
，使得
，則三個角
、
、
（ ）
A. 都是鈍角B. 至少有兩個鈍角
C. 恰有兩個鈍角D. 至多有兩個鈍角
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左焦點在拋物線
的準線上，且橢圓的短軸長為2，
分別為橢圓的左，右焦點，
分別為橢圓的左，右頂點，設點
在第一象限，且
軸，連接
交橢圓于點
，直線的斜率為
.
（Ⅰ）求橢圓的方程；
（Ⅱ）若三角形
的面積等于四邊形
的面積，求的值；
（Ⅲ）設點
為
的中點，射線
（
為原點）與橢圓交于點
，滿足
，求的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題p：函數f(x)＝x2＋2mx＋1在(－2，＋∞)上單調遞增；命題q：函數g(x)＝2x2＋2
(m－2)x＋1的圖象恒在x軸上方，若p∨q為真，p∧q為假，求m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
