
【題目】已知函數f(x)=|x2﹣2x﹣3|,若a<b<1,且f(a)=f(b),則u=2a+b的最小值為 .
【答案】3﹣2 ![]()
【解析】解:作出f(x)的圖象如圖,由圖可知,f(x)的對稱軸為:x=1.
∵a<b<1且f(a)=f(b),
∴a<﹣1,﹣1<b<1,
則|a2﹣2a﹣3|=|b2﹣2b﹣3|,
即a2﹣2a﹣3=﹣(b2﹣2b﹣3),
則(a﹣1)2+(b﹣1)2=8,a<﹣1,﹣1<b<1,
則(a,b)的軌跡是圓上的一個部分,(黑色部分),
由u=2a+b得b=﹣2a+u,
平移b=﹣2a+u,當直線b=﹣2a+u和圓在第三象限相切時,截距最小,此時u最小,
此時圓心(1,1)到直線2a+b﹣u=0的距離d= ![]() ,
,
即|u﹣3|=2 ![]() ,
,
得u=3﹣2 ![]() 或u=3+2
或u=3+2 ![]() (舍),
(舍),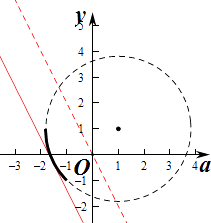
所以答案是:3﹣2 ![]()



科目:高中數學 來源: 題型:
【題目】橢圓![]() :
:![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,上頂點為
,上頂點為![]() ,下頂點為
,下頂點為![]() ,若直線
,若直線![]() 與直線
與直線![]() 的交點為
的交點為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)點![]() 為橢圓
為橢圓![]() 的長軸上的一個動點,過點
的長軸上的一個動點,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,證明:
兩點,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在物理實驗中,為了研究所掛物體的重量x對彈簧長度y的影響.某學生通過實驗測量得到物體的重量與彈簧長度的對比表:
物體重量(單位g) | 1 | 2 | 3 | 4 | 5 |
彈簧長度(單位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
(1)畫出散點圖;
(2)利用公式(公式見卷首)求y對x的回歸直線方程;
(3)預測所掛物體重量為8g時的彈簧長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
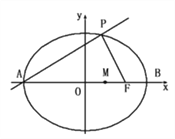
【題目】如圖,A、B分別是橢圓![]() 的左、右端點,F是橢圓的右焦點,點P在橢圓上,且位于x軸上方,PA⊥PF.
的左、右端點,F是橢圓的右焦點,點P在橢圓上,且位于x軸上方,PA⊥PF.
(1)點P的坐標;
(2)設M是橢圓長軸AB上的一點,M到直線AP的距離等于MB,求橢圓上的點到點M的距離d的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求數列{an}的通項公式.
(Ⅱ)設數列{bn}的前n項和為Tn,且Tn+![]() =λ(λ為常數),令cn=b2n(n∈N*).求數列{cn}的前n項和Rn.
=λ(λ為常數),令cn=b2n(n∈N*).求數列{cn}的前n項和Rn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M:(x﹣1)2+(y﹣1)2=4,直線l過點P(2,3)且與圓M交于A,B兩點,且|AB|=2 ![]() .
.
(1)求直線l方程;
(2)設Q(x0 , y0)為圓M上的點,求x02+y02的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,且兩個坐標系取相等的單位長度.已知直線
軸的正半軸為極軸,且兩個坐標系取相等的單位長度.已知直線![]() 的參數方程是
的參數方程是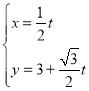 (
(![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,點
兩點,點![]() 為
為![]() 的中點,點
的中點,點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com